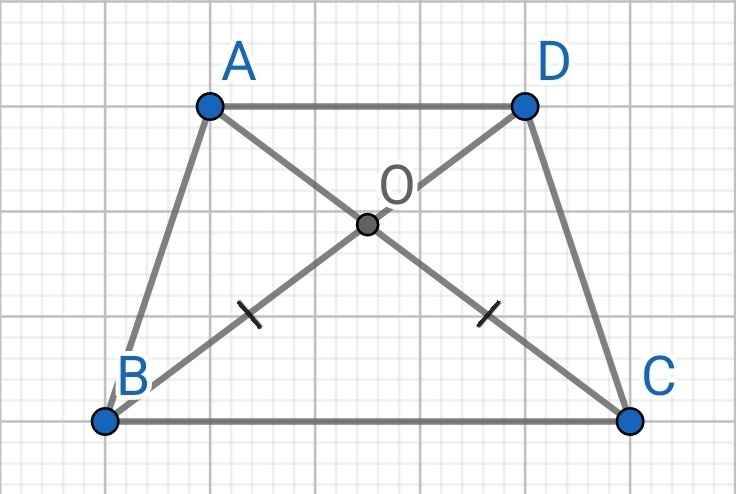
Cho hình thang ABCD
Hai đường chéo cắt nhau tại O ; gồm đường chéo AC và BD
Hãy tìm các tam giác bằng nhau .Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{DOC}\)
Do đó: ΔOAB\(\sim\)ΔOCD
Suy ra: OA/OC=OB/OD
hay \(OA\cdot OD=OB\cdot OC\)

 ∆OBC có:
∆OBC có:
OB = OC (gt)
⇒ ∆OBC cân tại O
⇒ ∠OBC = ∠OCB
Do ABCD là hình thang (AD // BC)
⇒ ∠OBC = ∠ODA (so le trong)
∠OCB = ∠OAD (so le trong)
Mà ∠OBC = ∠OCB (cmt)
⇒ ∠ODA = ∠OAD
∆OAD có:
∠ODA = ∠OAD (cmt)
⇒ ∆OAD cân tại O
⇒ OA = OD
Lại có:
OC = OB (gt)
⇒ OA + OC = OB + OD
⇒ AC = BD
⇒ ABCD là hình thang cân

Xét ΔADC có OM//DC
nên OM/DC=AM/AD
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC
Xét hình thang ABCD có MN//AB//CD
nên AM/AD=BN/BC
=>OM/DC=ON/DC
=>OM=ON
=>MN=2OM
OM//AB
=>OM/AB=DM/DA
OM//DC
=>OM/DC=AM/AD
=>OM/DC+OM/AB=DM/DA+AM/AD=1
=>1/AB+1/CD=1/OM
mà OM=1/2MN
nên 1/AB+1/CD=2/MN

Bạn tự vẽ hình nhé
Xét \(\Delta ACD\) có OE // CD(gt)
=> \(\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(1\right)\)
Xét \(\Delta BCD\) có OF // CD (gt)
=> \(\dfrac{OF}{DC}=\dfrac{BF}{FC}\left(2\right)\)
Mặt khác AB // CD nên \(\dfrac{AO}{AC}=\dfrac{BF}{FC}\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
=> \(\dfrac{OE}{DC}=\dfrac{OF}{DC}\) => OE = OF

Ta có: MN // AB (gt); AB // CD(gt) => MN // AB // CD
Xét tam giác ABC có: OM // AB (MN // AB)
=> \(\dfrac{OM}{AB}=\dfrac{CM}{CA}\) (hệ quả định lý Ta lét trong tam giác) (1)
Xét tam giác ABD có: ON // AB (MN // AB)
=> \(\dfrac{ON}{AB}=\dfrac{DN}{DB}\) (hệ quả định lý Ta lét trong tam giác) (2)
Xét hình thang ABCD có: MN // AB // CD (cmt)
=> \(\dfrac{CM}{CA}=\dfrac{DN}{DB}\) (định lý Ta lét trong hình thang) (3)
Từ (1) (2) (3) => OM = ON
\(\hept{\begin{cases}S_{ABC}=S_{BCD}\left(1\right)\\S_{AOB}=S_{COD}\left(2\right)\end{cases}}\)
Trước tiên ta chứng minh (1)
Hai tam giác ABC và BCD
- Có chiều cao bằng chiều cao hình thang
- Chung đáy BC
(2)
Tam giác ABC và BCD có chung tam giác BOC nên từ đó suy ra được
DT tam giác AOB = DT tam giác COD