2x2(x2+y2)+2y2(x2+y2)+5 (y2+x2) với x2+y2=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 8 2023
\(A=\left(2x^2+2y^2+5\right)\left(x^2+y^2\right)\)
=2x^2+2y^2+5
=2(x^2+y^2)+5
=2+5
=7
CM
16 tháng 6 2017
Ta xét các phương án:
(I) có:
(II) có:
(III) tương đương : x2+ y2 – 2x - 3y + 0,5= 0.
phương trình này có:
Vậy chỉ (I) và (III) là phương trình đường tròn.
Chọn D.
SS
17 tháng 8 2019
A= 2x^2 + y^2 - 2xy -2x+3
A= x^2-2xy + y^2 + x^2 - 2x+ 1 +2
A= (x-y)^2 + (x-1)^2 + 2
(x-y)^2> hoặc = 0 với mọi giá trị của x
(x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 > hoặc =0 với mọi giá trị của x
=> (x-y)^2 + (x-1)^2 + 2 > hoặc =2
=> A lớn hơn hoặc bằng 2
=> GTNN của A=2 tại x=y=1
2
9 tháng 5 2022
`x^2-2y^2+2/3x^2y^3+B=2x^2+y^2+2/3x^2y^3`
`=>B=2x^2+y^2+2/3x^2y^3-x^2+2y^2-2/3x^2y^3`
`=>B=(2x^2-x^2)+(y^2+2y^2)+(2/3x^2y^3-2/3x^2y^3)`
`=>B=x^2+3y^2`
Thay `x=1 ; y=[-1]/3` vào `B` có:
`B=1^2+3.([-1]/3)^2=1+3 . 1/9=1+1/3=4/3`
9 tháng 5 2022
`x^2 - 2y^2 + 2/3x^2y^3 + B = 2x^2 + y^2 + 2/3x^2y^3`
`=> B = 2x^2 + y^2 + 2/3x^2y^3` `- (x^2 - 2y^2 + 2/3x^2y^3)`
`= 2x^2 + y^2 + 2/3x^2y^3 - x^2 + 2y^2 - 2/3x^2y^3`
`= ( 2x^2 - x^2 ) + ( y^2 + 2y^2 ) + ( 2/3x^2y^3 - 2/3x^2y^3 )`
`= x^2 + 3y^2`
Thay `x=1 ; y=-1/3` vào `B` ta có `:`
`B = 1^2 + 3 . ( -1/3 )^2`
`= 1 + 1/3`
`= 4/3`
26 tháng 9 2021
\(C=\left(x^2-2xy+y^2\right)\left(x^2+y^2\right)-2x^3y-3x^3y^2+2xy^3\)
\(=\left(x^2+y^2\right)^2-2xy\left(x^2+y^2\right)-xy\left(2x^2+3x^2y+2y^2\right)\)
\(=\left(x^2+y^2\right)^2-xy\left(2x^2+2y^2+2x^2+3x^2y+2y^2\right)\)
\(=\left(x^2+y^2\right)^2-xy\left(4x^2+3x^2y+4y^2\right)\)
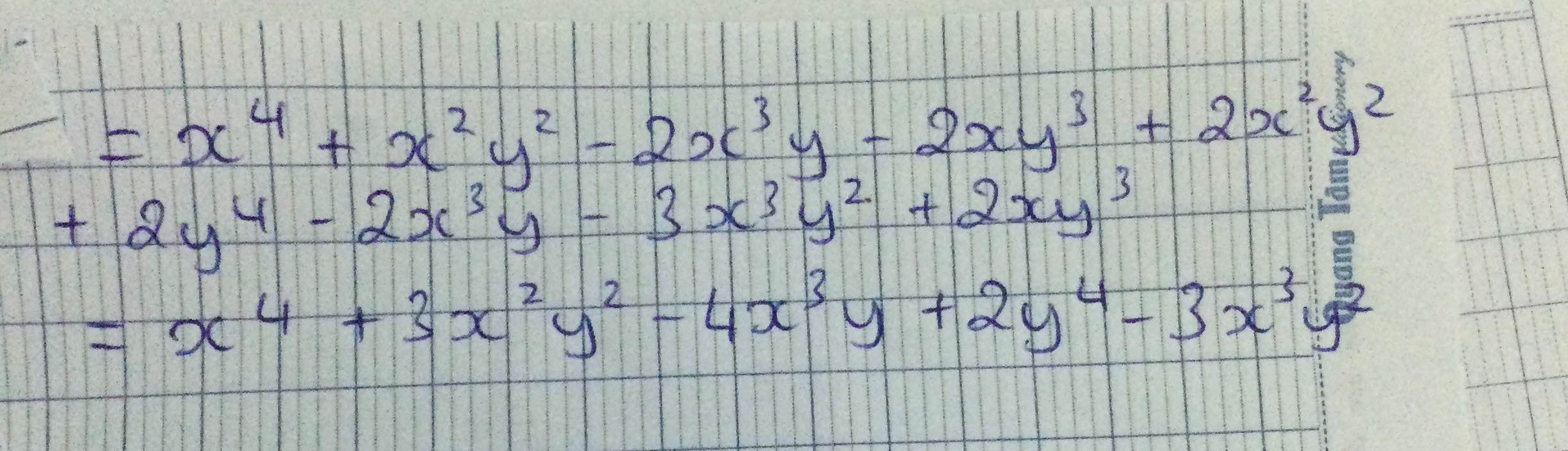
\(2x^2\left(x^2+y^2\right)+2y^2\left(x^2+y^2\right)+5\left(y^2+x^2\right)\)
\(=\left(x^2+y^2\right)\left(2x^2+2y^2\right)+5\left(x^2+y^2\right)\)
\(=2\left(x^2+y^2\right)\left(x^2+y^2\right)+5\left(x^2+y^2\right)\)
\(=2\left(x^2+y^2\right)^2+5\left(x^2+y^2\right)\)
Thay \(x^2+y^2=1\) vào ta có:
\(2\cdot1^2+5\cdot1=2+5=7\)