Luyện tập – Vận dụng 1
Cho hai ví dụ về hàm số mũ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
1
B
1
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
Ví dụ 1: \(y = 2{x^2} - x - 1\)
Ví dụ 2: \(y = - 3{x^2} + 1\)
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Ví dụ hàm số $y=\frac{-1}{2}x$
Ta có bảng sau:
Với mỗi giá trị của x ta có 1 giá trị của y, vậy bảng trên biểu thị cho 1 hàm số
Tập xác định của hàm số \(D = \left\{ { - 2; - 1; - \frac{1}{2};0;\frac{1}{2};1;2} \right\}\)
Tập giá trị của hàm số \(\left\{ {1;\frac{1}{2};\frac{1}{4};0; - \frac{1}{4}; - \frac{1}{2}; - 1} \right\}\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
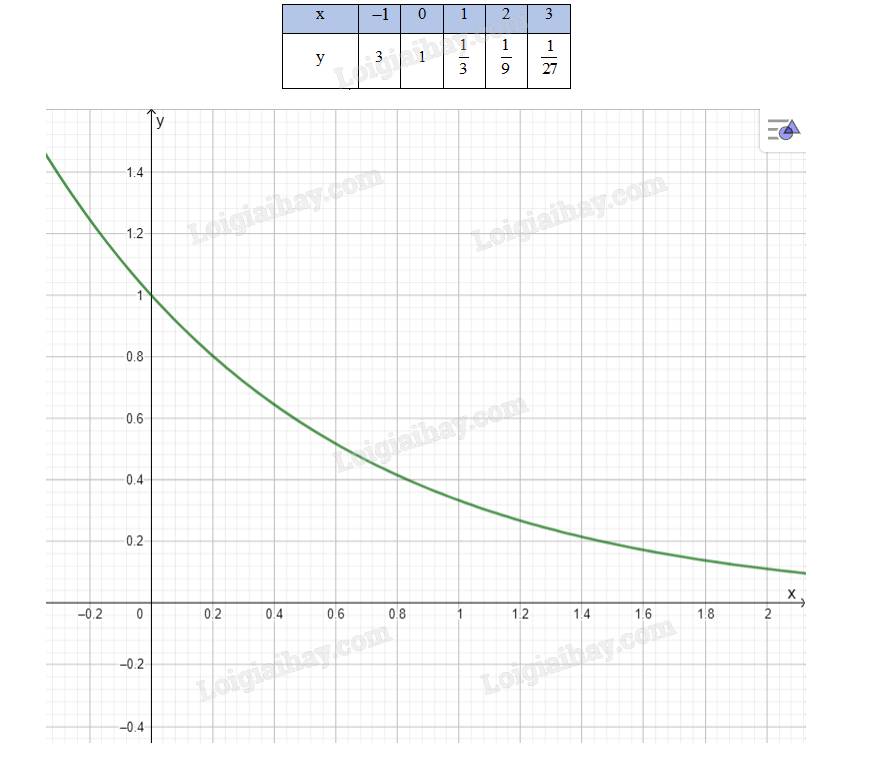
\(\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{1}{3}} \right)^x} = 0;\,\,\mathop {\lim }\limits_{x \to - \infty } {\left( {\frac{1}{3}} \right)^x} = + \infty \)
Hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) nghịch biến trên toàn R
Bảng biến thiên của hàm số:
Đồ thị hàm số:
\(y=2^{2x};y=5^x\)
\(y=3^x;y=5^{x+3}\)