K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
B
1
B
1
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
\(\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{1}{3}} \right)^x} = 0;\,\,\mathop {\lim }\limits_{x \to - \infty } {\left( {\frac{1}{3}} \right)^x} = + \infty \)
Hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) nghịch biến trên toàn R
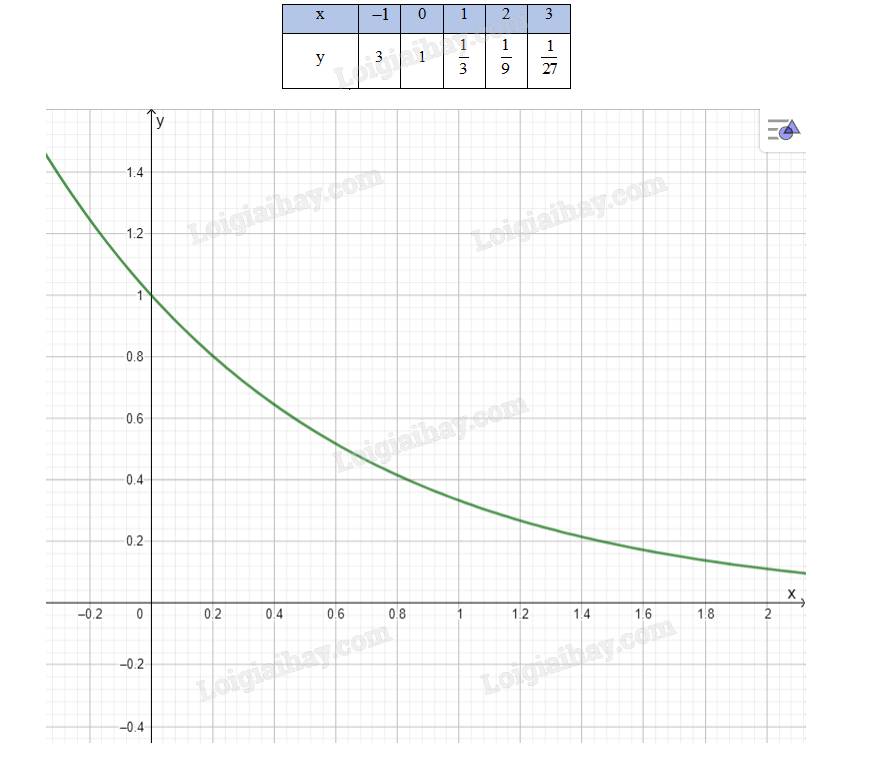
Bảng biến thiên của hàm số:
Đồ thị hàm số:
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ví dụ về hàm số tuần hoàn là : \(g(x) = \left\{ \begin{array}{l}0\,\,\,\,\,\,\,,x \in Q\\1\,\,\,\,\,\,\,\,,x \in R\end{array} \right.\)
CM
21 tháng 11 2018
Xét hàm số
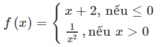
- Trường hợp x ≤ 0
f(x) = x + 2 là hàm đa thức, liên tục trên R nên nó liên tục trên (-2; 0]
- Trường hợp x > 0
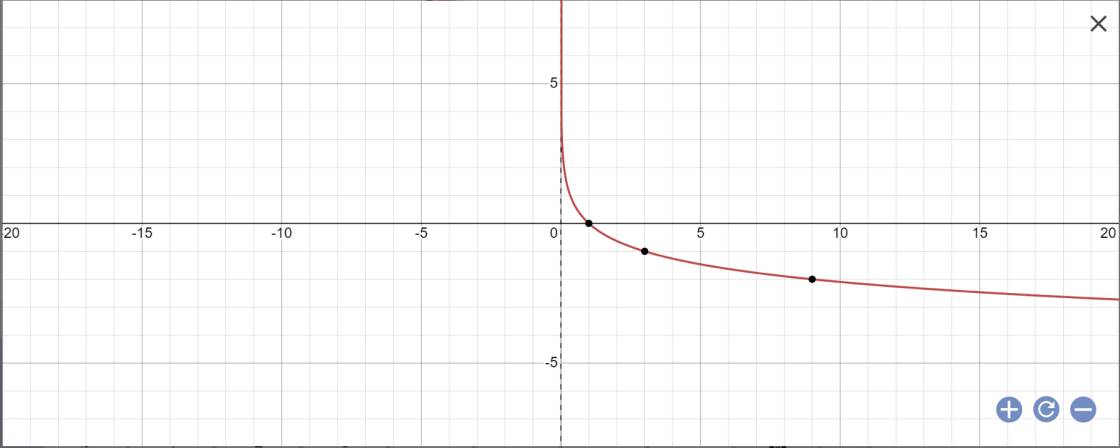
f ( x ) = 1 / x 2 là hàm số phân thức hữu tỉ nên liên tục trên (2; 0) thuộc tập xác định của nó.
Như vậy f(x) liên tục trên (-2; 0] và trên (0; 2)
Tuy nhiên, vì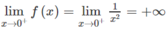 
nên hàm số f(x) không cógiới hạn hữu hạn tại x = 0. Do đó, nó không liên tục tại x = 0. Nghĩa là không liên tục trên (-2; 2)
B
1
14 tháng 8 2023
2;-2 là căn bậc 6 của 64 vì \(2^6=64;\left(-2\right)^6=64\)
\(log_2x;log_3y\)
\(log_3x;log_5\left(x+2\right)\)