Trong mặt phẳng tạo độ 0xy,cho parabol p ; \(y=x^2\) và đường thẳng d ; \(y=2x+3\)
Chứng minh rằng d và p có 2 điểm chung phân biệt
AI GIÚP MÌNH VƠI . MÌNH CẢM ƠN Ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ Parabol P : y = 2 x 2
Bảng giá trị giữa x và y:
x |
-2 |
-1 |
0 |
1 |
2 |
y |
8 |
2 |
0 |
2 |
8 |
Vẽ đúng đồ thị

đầu tiên viết pt hoành độ giao điểm
thứ hai giải denta của pt hoành độ giao điểm để tìm điều kiện của m
thứ ba giải viet rồi thế x1x2 vào pt mà đề cho
thứ tư vì y1 và y2 đều thuộc (d) nên y1 = 2x1 - m + 1
y2 = 2x2 - m + 1
thứ năm thay y1 và y2 vào pt mà đề cho rồi giải tìm m và m sẽ bằng 7 (thỏa mãn đk của denta)

Phương trình d' qua M và vuông góc d có dạng:
\(2\left(x-2\right)+1\left(y+2\right)=0\Leftrightarrow2x+y-2=0\)
Hình chiếu vuông góc của M lên d là giao điểm d và d' nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x-2y+1=0\\2x+y-2=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=\dfrac{4}{5}\end{matrix}\right.\) \(\Rightarrow\left(\dfrac{3}{5};\dfrac{4}{5}\right)\)

`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
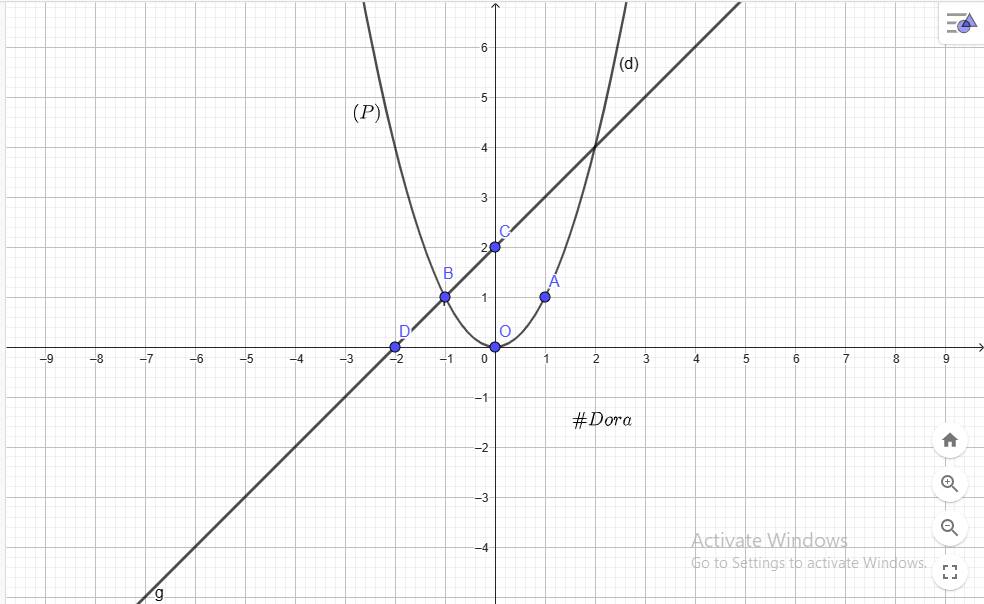
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`

AB=(3;-1)
AC=(4;2)
AB.AC= |AB|.|AC|.cos(AB,AC)
cos( AB,AC)= \(\dfrac{10}{\sqrt{10}.2\sqrt{5}}=\dfrac{\sqrt{2}}{2}\)
BAC=45

b: Phương trình hoành độ giao điểm là:
\(x^2-5x+m^2-4=0\)
Để (d) cắt (P) tại hai điểm nằm khác phía so với trục tung thì (m-2)(m+2)<0
=>-2<m<2