M nằm trong góc xOy=30 độ,khoảng cách từ M đến Ox, Oy là MH=1, MK= \(\sqrt{3}\)
a) ch/m KH=OM*sinO
b) Tính góc MOx
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 8 2019
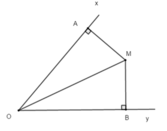
Gọi MA và MB theo thứ tự là khoảng cách từ M đến Ox và Oy
Xét hai tam giác vuông OMA và OMB có:
OM là cạnh chung
MA = MB (gt)
Do đó ΔOMA=ΔOMB (cạnh huyền – cạnh góc vuông)
Suy ra: M O A ^ = M O B ^ (hai góc tương ứng)
Vậy OM là tia phân giác của x O y ^
Vậy thứ tự sắp xếp phải là: b, c, a, d, e.
Chọn đáp án A
VT
2 tháng 4 2019
Đáp án C
Phương pháp: Δ φ = 2 π d λ
Cách giải:
+ Áp dụng hệ thức lượng trong tam giác vuông OMN có đường cao OH:
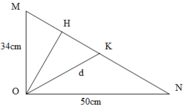
1 O H 2 = 1 O M 2 + 1 O N 2 ⇔ 1 O H 2 = 1 34 2 + 1 50 2 ⇒ O H = 28,1 c m
+ Gọi d là khoảng cách từ O đến K (K là 1 điểm bất kì trên MN)
+ Độ lệch pha giữa K và O là: Δ φ = 2 π d λ
+ Để K dao động cùng pha với O thì: Δ φ = 2 π d λ = 2 k π ⇒ d = k λ
+ Số điểm dao động cùng pha với o trên đoạn MN bằng số giá trị k nguyên thoả mãn:
28,1 ≤ k λ ≤ 34 ⇒ 7,025 ≤ k ≤ 8,5 ⇒ k = 8 28,1 < k λ ≤ 50 ⇒ 7,025 < k ≤ 12,5 ⇒ k = 8 ; 9 ; 10 ; 11 ; 12
Có 6 giá trị của k thoả mãn ⇒ trên đoạn MN có 6 điểm dao động cùng pha với nguồn
BN
4
14 tháng 1 2017
vì ta Oz nằm giữa Ox và Oy
\(\Rightarrow\widehat{xOz}+\widehat{zOy}=\widehat{xOy}\)
Hay \(b^o+\widehat{zOy}=a^o\)
\(\Rightarrow\widehat{zOy}=a^o-b^o\)
KL \(\widehat{zOy}=a^o-b^o\)