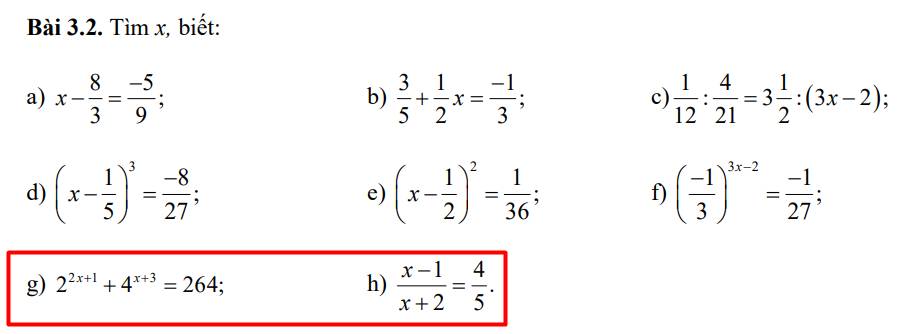
Câu G và H nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Sai
Cho ba điểm bất kì thẳng hàng thì chỉ có đúng 1 điểm nằm giữa hai điểm còn lại.

b. Đúng

c. Đúng


\(G=\left(x^2-2xy+y^2\right)+\left(x^2-2x+1\right)+8=\left(x-y\right)^2+\left(x-1\right)^2+8\)
=> GTNN của G là 8
\(H=\left(x^2-4x+4\right)+\left(y^2+6y+9\right)+7=\left(x-2\right)^2+\left(y+3\right)^2+7\)
=> GTNN của H là 7
\(K=\left(x^2-4x+4\right)+\left(y^2+2y+1\right)+\left(z^2-6z+9\right)+26=\left(x-2\right)^2+\left(y+1\right)^2+\left(z-3\right)^2+26\)
=> GTNN của K là 26

e: Ta có: \(E=\sqrt{19+8\sqrt{3}}-\sqrt{28-6\sqrt{3}}+\sqrt{12}\)
\(=4+\sqrt{3}-3\sqrt{3}+1+2\sqrt{3}\)
=5

Bài 5:
i: \(x^2-9x+8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=8\end{matrix}\right.\)

Bài 6:
a: \(M=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)

a: \(x\left(x-1\right)-x^2+4x=-3\)
\(\Leftrightarrow x^2-x-x^2+4x=-3\)
hay x=-1
\(G=2^{2x+1}+4^{x+3}=264\\\Leftrightarrow 2^{2x+1}+\left(2^2\right)^{x+3}=264\\ \Leftrightarrow2^{2x+1}+2^{2x+6}=264\\ \Leftrightarrow2^{2x+1}\left(1+2^5\right)=264\\ \Leftrightarrow2^{2x+1}.33=264\\ \Leftrightarrow2^{2x+1}=\dfrac{264}{33}=8=2^3\\ Vậy:2x+1=3\\ \Rightarrow2x=3-1=2\\ x=\dfrac{2}{2}=1\\ Vậy:x=1\)
___
\(h,\dfrac{x-1}{x+2}=\dfrac{4}{5}\left(ĐK:x\ne2\right)\\ \Rightarrow5\left(x-1\right)=4\left(x+2\right)\\ \Leftrightarrow5x-4x=8+5\\ \Leftrightarrow x=13\\ Vậy:x=13\)