Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AB = AD.
a) Chứng minh tam giác ABC = tam giác ADC.
b) Từ A kẻ vuông góc với BC tại K, kẻ AH vuông góc với DC tại H, chứng minh AH = AK.
c) Kéo dài KA cắt tia CD tại M, kéo dài HA cắt tia CB tại N. Gọi I là trung điểm của MN, chứng minh C, A, I thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó: ΔABC=ΔADC
b: Xét ΔCDH vuông tại D và ΔCBH vuông tại B có
CH chung
CD=CB
Do đó: ΔCDH=ΔCBH
Suy ra: DH=BH

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC

t lười vẽ hình lắm, vô cùng xin lỗi :(
a) Vì ∆ ABC cân tại A nên AH vừa là đường cao, vừa là trung tuyến => HB = HC = 12:2 = 6
Áp dụng định lí Py-ta-go cho ∆ AHB, ta được: AH2 + BH2 = AB2 => AB2 = 122 + 92 = 225 = 152 => AB = 15 = AC
=> PABC = AB + AC + BC = 15 + 15 + 18 = 48
b) Vì BM = CN (gt) ; HB = HC (cmt) => HB + BM = HC + CN => HM = HN => AH là trung tuyến của ∆ AMN (1)
Lại có: AH ┴ BC hay AH ┴ MN => AH là đường cao của ∆ AMN (2)
Từ (1) và (2) =>∆ AMN cân tại A
c) Xét ∆ BIM và ∆ CKN vuông tại I và K có:
MB = NC (gt) ; ^KNC = ^IMB (∆AMN cân tại A) => ∆ BIM = ∆ CKN ( ch - gn ) => MI = KN
Mà AM = AN (∆AMN cân tại A) => AI = AK => ∆ AIK cân tại A
=> ^AIK = ^AKI = ( 180o - ^MAN ) : 2 = ^AMN = ^ANM => IK // MN (đồng vị) hay IK // BC
d) Vì IK // MN => ^IKN = ^KCN (slt) ; ^KIB = ^IBM (slt)
Lại có: ^IBM = ^KCN ( vì ∆BIM=∆CKN ) => ^IKN = ^KIB hay ^OIK = ^OKI => ∆OKI cân tại O => OK = OI
Xét ∆ AIO và ∆ AKO có:
AI = AK ( ∆AIK cân tại A) ; OK = OI (cmt) ; AO (chung) => ∆ AIO = ∆ AKO ( c-c-c )
=> ^OAI = ^OAK (3)
Vì ∆AMN cân tại A => AH là phân giác của ∆AMN.=> ^HAM = ^HAN hay ^HAI = ^HAK (4)
Từ (3) và (4) => A, O, H thẳng hàng.
Ya, that's it!

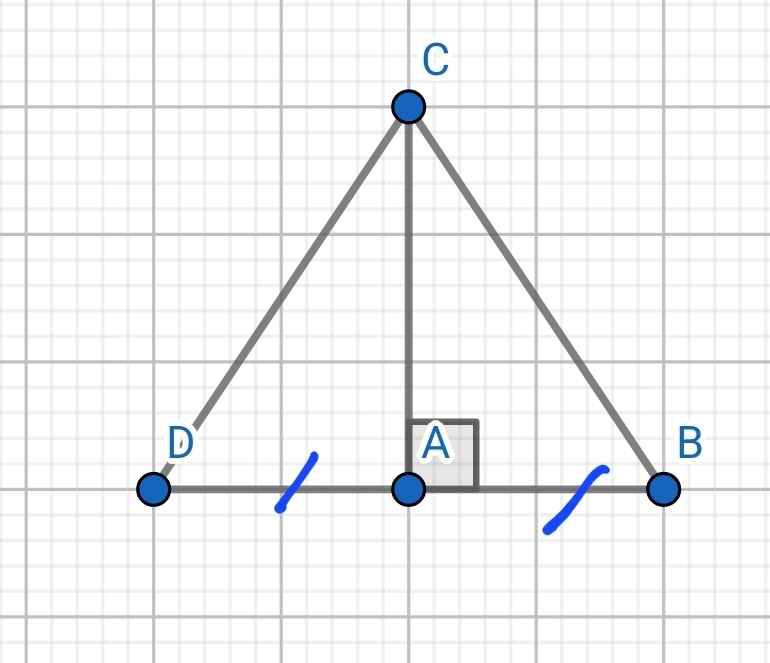
a) Xét hai tam giác vuông: ∆ABC và ∆ADC có:
AC chung
AB = AD (gt)
⇒ ∆ABC = ∆ADC (hai cạnh góc vuông)
b) Do ∆ABC = ∆ADC (cmt)
⇒ ∠BCA = ∠DCA (hai góc tương ứng)
⇒ CA là tia phân giác của ∠BCD

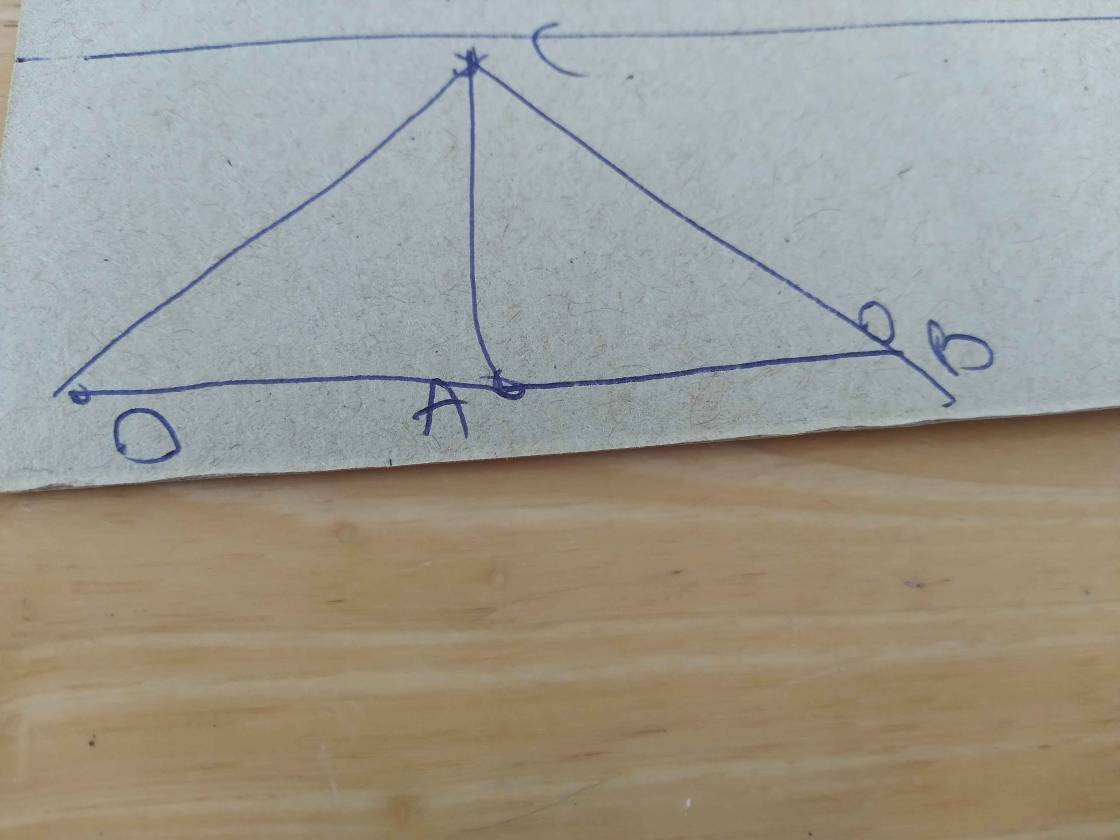
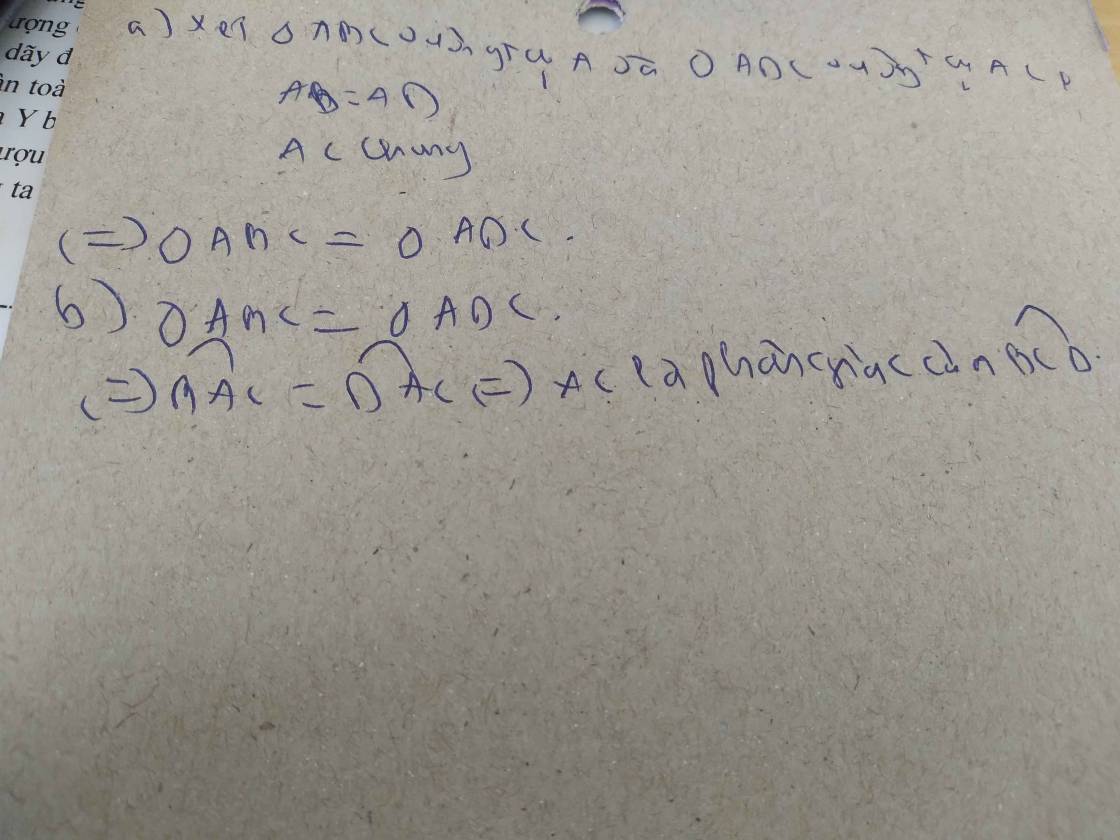
a: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AC chung
AB=AD
=>ΔABC=ΔADC
b: ΔABC=ΔADC
=>góc DCA=góc BCA
Xét ΔCHA vuông tại H và ΔCKA vuông tại K có
CA chung
góc HCA=góc KCA
=>ΔCHA=ΔCKA
=>AH=AK
c: Xét ΔHAM vuông tại H và ΔKAN vuông tại K có
AH=AK
góc HAM=góc KAN
=>ΔHAM=ΔKAN
=>AM=AN và HM=KN
CH+HM=CM
CK+KN=CN
mà CH=CK và HM=KN
nên CM=CN
CM=CN
AM=AN
=>CA là trung trực của MN
=>C,A,I thẳng hàng