Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
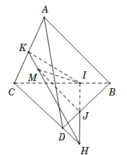
Trong mặt phẳng (BCD); IJ cắt CD tại H nên H thuộc (ACD)
Điểm H thuộc IJ m suy ra bốn điểm M; I; J; H đồng phẳng.
Nên trong mặt phẳng (IJM) , MH cắt IJ tại H và M H ⊂ I J M .
Mặt khác M ∈ A C D H ∈ A C D ⇒ M H ⊂ A C D .
Vậy giao tuyến của 2 mặt phẳng (ACD) và ( IJM) là MH
Chọn D.
Trong mp (ACD), kéo dài IJ cắt CD tại E thì E là giao điểm của CD và (IJK)
Ta có
\(E\in MN\) mà \(MN\in\left(OMN\right)\Rightarrow E\in\left(OMN\right)\)
\(O\in\left(OMN\right)\)
\(\Rightarrow EO\in\left(OMN\right)\)
Ta có
\(E\in BD\) mà \(BD\in\left(BCD\right)\Rightarrow E\in\left(BCD\right)\)
\(O\in\left(BCD\right)\)
\(EO\in\left(BCD\right)\)
Trong (BCD) kéo dài EO cắt CD tại K
=> \(K\in\left(OMN\right);K\in CD\) => K chính là giao của CD với (OMN)
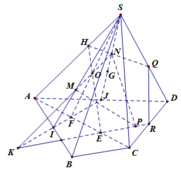
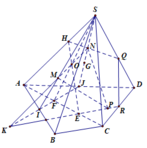
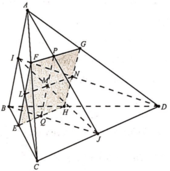
Gọi E là giao của AI với BC
F là giao của AJ với BD
Gọi M là giao của EF và BM
Chọn mp(AFE) có chứa IJ
FE cắt BM tại N
nên \(N\in\left(ABM\right)\cap\left(AFE\right)\)
=>(ABM) giao (AFE)=AN
Gọi giao của AN với IJ là K
=>K là giao của JI với (AMB)