Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Kẻ đường thẳng qua C song song với BM cắt BD ở G, AG cắt DN ở J, đường thẳng qua J song song với CG cắt AC ở I.
Kẻ AH vuông góc với BD tại H.
Dễ dàng chứng minh được IJ//BM; B là trung điểm của GD và tính được
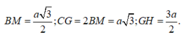
Ta có: Tam giác ANJ đồng dạng với tam giác AHG nên:

Mà IJ//CG nên:
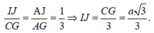

Đáp án C
Ta dễ dàng chứng minh được I A → + I B → + I C → + I D → = 0 → nên k = 1.
Thật vậy ta có
![]()

a) Vì I là trọng tâm của tam giác ABD nên \(AI=\dfrac{1}{3}AC\)


Đáp án B
Ta dễ có:
M N → = M A → + A D → + D N → M N → = M B → + B C → + C N →
![]()
Mà M và N lần lượt là trung điểm của AB và CD nên
![]()
Do đó 2 M N → = A D → + B C →
![]()
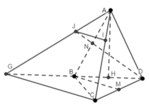
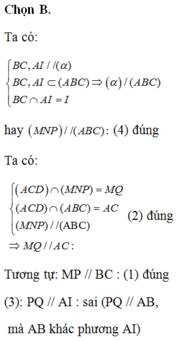
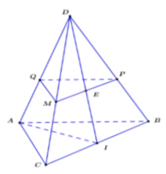
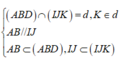
Gọi E là giao của AI với BC
F là giao của AJ với BD
Gọi M là giao của EF và BM
Chọn mp(AFE) có chứa IJ
FE cắt BM tại N
nên \(N\in\left(ABM\right)\cap\left(AFE\right)\)
=>(ABM) giao (AFE)=AN
Gọi giao của AN với IJ là K
=>K là giao của JI với (AMB)