![]() mink sắp học r
mink sắp học r
giúp mink với
Vòi nước thứ nhất chảy đầy một bể cạn trong 45 phút. Vòi nước thứ hai nếu chảy trong 12 phút thì được 1 /3 bể. Hỏi nếu bể cạn, mở cả hai vòi một lúc thì sau bao lâu bể đầy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1 phút vòi 1 chảy được: 1 : 45 = \(\dfrac{1}{45}\) (bể)
1 phút vòi hai chảy được: \(\dfrac{1}{3}\) : 12 = \(\dfrac{1}{36}\) (bể)
1 phút hai vòi cùng chảy được: \(\dfrac{1}{45}\) + \(\dfrac{1}{36}\) = \(\dfrac{1}{20}\)(bể)
Hai vòi cùng chảy đầy bể sau: 1 : \(\dfrac{1}{20}\) = 20 (phút)
Đáp số: 20 phút

bai 6:
P/S chi so phan be voi thu nhat chay trong 1 gio la:
1:5=1/5(be)
P/S chi so phan be voi thu hai chay trong 1 gio la:
1:7=1/7(be)
P/S chi so phan be trong 1 gio ca hai voi cung chay la:
1/5+1/7=12/35(be)
neu hai voi cung chay thi sau:
1:12/35=2gio 55 phut
minh chi lam vay thoi chu lam het thi lau lam
Đầu bài ở dạng vòi nước chảy vào bể thì ta tạm chấp nhập logic lượng nước chảy vào là hằng số (hằng số trên 1 đơn vị thời gian).
Trong thực tế vòi nước tháo ra: áp xuất trong bể càng lớn (lượng nước trong bể càng nhiều) thì lượng nước tháo ra càng nhiều. do đó cần bổ xung thêm đầu bài là lượng nước tháo ra cũng là hằng số (hằng số trên 1 đơn vị thời gian)

Gọi thời gian chảy một mình đầy bể của vòi 1 và vòi 2 lần lượt là a,b
Theo đề, ta có hệ:
1/a+1/b=1/1,5 và 1/4*1/a+1/3*1/b=1/5
=>a=15/4 và b=5/2

Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là x (giờ), (x > 0)
Trong một giờ:
- Vòi thứ nhất chảy được 1/x (bể)
- Vòi thứ hai chảy được 1/(x+4) (bể)
- Vòi thứ ba chảy được 1/6 (bể)
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước ở bể chảy ra nên ta có phương trình:
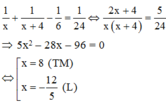
Vậy chỉ dùng vòi thứ nhất thì sau 8 giờ bể đầy nước
Đáp án: D

- Gọi phần bể vòi thứ nhất, thứ hai chảy được trong 1 phút lần lượt là \(x,y\left(0< x,y< 1\right)\)
Đổi 1h30p=90p
- Hai vòi nước cùng chảy vào 1 bể cạn thì sau 1h30p đầy bể nên:
\(90\left(x+y\right)=1\Rightarrow x+y=\dfrac{1}{90}\left(1\right)\)
- Vòi 1 chảy trong 15p rồi đến vòi 2 chảy tiếp trong 20p được 1/5 bể nên:
\(15x+20y=\dfrac{1}{5}\left(2\right)\)
(1), (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=\dfrac{1}{90}\\15x+20y=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15x+15y=\dfrac{1}{6}\\15x+20y=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=\dfrac{1}{90}\\5y=\dfrac{1}{30}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{225}\\y=\dfrac{1}{150}\end{matrix}\right.\)
Thời gian vòi 1 chảy để đầy bể: \(1:\dfrac{1}{225}=225\) phút = 3,75h.
Thời gian vòi 2 chảy để đầy bể: \(1:\dfrac{1}{150}=150\) phút=2,5h.
Để giải quyết bài toán này, chúng ta cần xác định lượng nước mà mỗi vòi chảy vào bể trong một giờ.
Gọi x là lượng nước mà mỗi vòi chảy vào bể trong một giờ. Theo giả thiết, khi mở cả hai vòi trong một giờ, bể sẽ được 1/3 đầy. Vì vậy, lượng nước mà mỗi vòi chảy vào bể trong một giờ là 2x (do có hai vòi).
Theo giả thiết ban đầu, nếu hai vòi cùng chảy vào bể trong 6 giờ, bể sẽ đầy. Với lượng nước mà mỗi vòi chảy vào bể trong một giờ là 2x, ta có:
6 * 2x = 1 (bể đầy)
Từ đó, ta có:
12x = 1
x = 1/12
Vậy, mỗi vòi chảy riêng thì để bể đầy, mỗi vòi sẽ mất 1/12 giờ, hay khoảng 5 phút.
Lưu ý rằng đây là một bài toán giả định, và kết quả phụ thuộc vào giả thiết ban đầu.

Câu hỏi của mẹ má mài - Toán lớp 5 - Học toán với OnlineMath Em tham khảo nhé!

Vòi thứ nhất 1 giờ chảy được số phần bể là :
1 : 3 = \(\frac{1}{3}\)( bể )
Vòi thứ hai 1 giờ chảy được số phần bể là :
1 : 6 = \(\frac{1}{6}\)( bể )
Vòi thứ ba 1 giờ chảy được số phần bể là :
1 : 8 = \(\frac{1}{8}\)( bể )
Nếu mở cả 3 vòi thì sau số thời gian sẽ đầy bể là :
\(1\div\left(\frac{1}{3}+\frac{1}{6}+\frac{1}{8}\right)=\frac{8}{5}\)( giờ )
Đổi : \(\frac{8}{5}\)giờ = 1 giờ 36 phút
Đ/S : 1 giờ 36 phút

Đổi 2 giờ 55 phút = ![]() giờ
giờ
Gọi x (giờ) là thời gian chảy riêng đầy bể của vòi thứ nhất.
Điều kiện: x > 35/12
Khi đó thời gian chảy riêng đầy bể của vòi thứ hai là x + 2 (giờ)
trong 1 giờ, vòi thứ nhất chảy được 1/x (bể)
trong 1 giờ, vòi thứ hai chảy được 1/(x + 2 ) (bể)

Giá trị x = - 7/6 không thỏa mãn điều kiện bài toán.
Vậy vòi thứ nhất chảy riêng đầy bể trong 5 giờ
vòi thứ hai chảy riêng đầy bể trong 5 + 2 = 7 giờ
Đổi ; \(45p=\dfrac{3}{4}h\)
Vòi 2 chảy số h để đầy bể là ; \(12\times3=36p=\dfrac{3}{5}h\)
1h 2 vòi chảy dc: \(1\div\dfrac{3}{4}+1\div\dfrac{3}{5}=3\) bể
Vậy 2 vòi chảy chung 1 bể trong : \(1\div3=\dfrac{1}{3}h\)
Đổi `45` phút `=3/4` giờ
Thời gian vòi `2` chảy đầy bể là :
`12xx3=36` ( Phút )
Đổi `36` Phút `=3/5` Giờ
`1` giờ , cả hai vòi chảy được số bể là :
`(1:3/4)+(1:3/5)=3` ( bể )
Nếu bể cạn , mở cả 2 `2` vòi chảy chung trong thời gian :
`1:3=1/3` giờ
Đáp số : `1/3` giờ