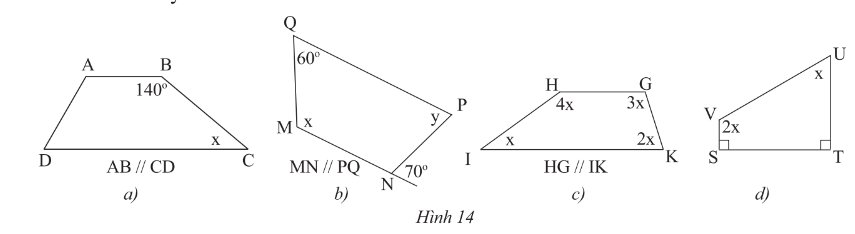
Tìm \(x\) và \(y\) ở các hình sau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Mìk tính y :

Vì tứ giác CDPQ có hai góc vuông và hai cạnh CD = DP = 4 nên nó là hình vuông. Suy ra: CD = DP = PQ = QC = 4
Trong tam giác vuông BCQ, ta có:
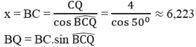
≈ 6,223.sin 50 ° = 4,767
Trong tam giác vuông ADP, ta có:
AP = DP.cotgA = 4.cotg 70 ° ≈ 1,456
Ta có: y = AB = AP + PQ + QB = 1,456 + 4 + 4,767 = 10,223

Chọn C
(1) Sau 1 phút, khí H2 thoát ra ở bình X nhiều hơn ở bình Y
(4) Sau 10 phút, khí H2 thoát ra ở 2 bình X và Y bằng nhau

- Cách vẽ:
+ Cho x = 1 ta được y = √3.1 = √3
+ Dựng điểm A(1; √3 ). Vẽ đường thẳng qua O, A được đồ thị hàm số y = √3 x.
- Các bước vẽ đồ thị hàm số y = √3 x.
+ Dựng điểm B(1; 1). Vẽ OB ta được
![]()
+ Dựng điểm √2 trên trục hoành Ox: vẽ cung tròn bán kính OC = √2, cắt Ox tạ điểm có hoành độ là √2.
+ Dựng điểm D(√2; 1). Vẽ OD ta được
![]()
+ Dựng điểm √3 trên trục tung Ox: Vẽ cung tròn bán kính OD = √3 cắt Oy tại điểm có tung độ là √3.
+ Dựng điểm A(1; √3)
+ Vẽ đường thẳng O, A ta được đồ thị hàm số y = √3 x.
a) Vì \(AB\) // \(CD\) (gt) suy ra:
\(\widehat B + \widehat C = 180^\circ \) (cặp góc trong cùng phía)
\(\begin{array}{l}140^\circ + x = 180^\circ \\x = 40^\circ \end{array}\)
b) Vì \(MN\) // \(PQ\) (gt)
\( \Rightarrow \widehat M + \widehat Q = 180^\circ \) (trong cùng phía)
\(\begin{array}{l}x + 60^\circ = 180^\circ \\x = 120^\circ \end{array}\)
Vì \(MN\) // \(PQ\) (gt)
\( \Rightarrow \widehat P = \widehat N = 70^\circ \) (so le trong)
c) Xét tứ giác \(IHGK\) ta có:
\(\begin{array}{l}\widehat H + \widehat G + \widehat I + \widehat K = 360^\circ \\4x + 3x + 2x + x = 360^\circ \\10x = 360^\circ \\x = 360^\circ :10 = 36^\circ \end{array}\)
d) Xét tứ giác \(UVST\) ta có:
\(\widehat U + \widehat V + \widehat S + \widehat T = 360^\circ \)
\(\begin{array}{l}x + 2x + 90^\circ + 90^\circ = 360^\circ \\3x + 180^\circ = 360^\circ \\3x = 180^\circ \\x = 60^\circ \end{array}\)