Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
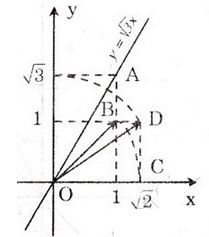
Ta có: \(\sqrt{3}\) = \(\sqrt{2+1}\) = \(\sqrt{\left(\sqrt{2}\right)^2+1^2}\)
Hình vẽ SGK có : OC = OB = \(\sqrt{2}\) và theo định lí Py-ta-go t a có :
OD = \(\sqrt{OC^2+CD^2}\)= \(\sqrt{\left(\sqrt{2}\right)^2+1^2}\)= \(\sqrt{3}\)
Dùng compa ta xác định được điểm biểu diễn số \(\sqrt{3}\). trên Oy. Từ đó xác định được điểm A.
Hướng dẫn giải:
∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diện tích tam giác đều cạnh a là a2√44 ta có
S∆OBC = SΔOBC=R2√34 (1)
Diện tích hình quạt tròn AOB là:
π.R2.6003600=πR26 (2)
Từ (1) và (2) suy ra diện tích hình viên phân là:
πR26−R2√34=R2(π6−√34)
Thay R = 5,1 ta có Sviên phân ≈ 2,4 (cm2)
a) Ta có: x² = 4.9 = 36 => x = 6
b) Ta có: * 2² = x.x => x² = 4 => x = 2
* y² = x(x + x) = 2.4 = 8 => y = 2√2
c) Ta có: 12² = x.16 => x = 144/16 = 9
Vậy x = 9
y² = x(x + 16) = 6(9 + 16) = 9.25 = 225 => y = 15
a) Dùng hệ thức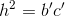 
. Đáp số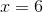 
b) Dùng hệ thức 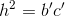tính được 
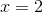. Để tìm y, có thể dùng hệ thức 
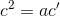hoặc định lý Py-ta-go. ĐS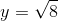 
c) Dùng hệ thức 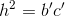tính được 
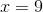từ đó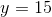 
.
a) Áp dụng hệ thức lượng trong tam giác vuông⇒32=2x⇒x=\(\dfrac{9}{2}=4,5\)
Áp dụng định lý Pi-ta-go⇒y2=32+x2=9+20,25=29,25⇒\(y=\dfrac{3\sqrt{13}}{2}\)
b) Ta có \(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AC=\dfrac{4}{3}.AB=\dfrac{4}{3}.15=20\)
Áp dụng hệ thức lượng trong tam giác vuông ⇒\(\dfrac{1}{x^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{225}+\dfrac{1}{400}=\dfrac{1}{144}\Rightarrow x^2=144\Rightarrow x=12\)Áp dụng hệ thức lượng trong tam giác vuông ⇒AB.AC=x.y⇒\(y=\dfrac{AB.AC}{x}=\dfrac{15.20}{12}=25\)
a) Hình a
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
x2=2.(2+6)=2.8=16 ⇒x=4x2=2.(2+6)=2.8=16⇒x=4
y2=6.(2+6)=6.8=48⇒y=√48=4√3y2=6.(2+6)=6.8=48⇒y=48=43
b) Hình b
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có:
x2=2.8=16⇒x=4
