Tứ giác \(ABCD\) có góc ngoài tại đỉnh \(A\) bằng \(65^\circ \), góc ngoài tại đỉnh \(B\) bằng \(100^\circ \), góc ngoài tại đỉnh \(C\) bằng \(60^\circ \). Tính số đo góc ngoài tại đỉnh \(D\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 7 2023
Gọi góc ngoài đỉnh B là x
Ta có:
$\widehat {B} + x = 180^0 $
`=>`$ \widehat {B} + 110^0 = 180^0$
`=>` $\widehat {B} = 70^0$
Xét tứ giác ABCD:
$\widehat {A} + \widehat {B} + \widehat {C} + \widehat {D}= 360^0$
`=>` $100^0 + 70^0 + 75^0 + \widehat {D} = 360^0$
`=>` $\widehat {D} = 115^0$
Vậy, $\widehat {D} = 115^0.$
CM
11 tháng 10 2017
Đáp án cần chọn là: A
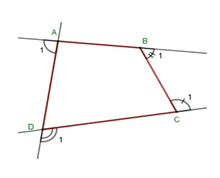
Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là A 1 ^ ; B 1 ^ ; C 1 ^ ; D 1 ^ .
Khi đó ta có :
A ^ + A 1 ^ = 180 ° ⇒ A 1 ^ = 180 ° - A ^ ; B ^ + B 1 ^ = 180 ° ⇒ B 1 ^ = 180 ° - B ^ ; C ^ + C 1 ^ = 180 ° ⇒ C 1 ^ = 180 ° - C ^ ; D ^ + D 1 ^ = 180 ° ⇒ D 1 ^ = 180 ° - D ^ ;
Suy ra
A 1 ^ + B 1 ^ + C 1 ^ + D 1 ^ = 180 ° - A ^ + 180 ° - B ^ + 180 ° - C ^ + 180 ° - D ^ = 720 ° - A ^ + B ^ + C ^ + D ^ = 720 ° - 360 ° = 360 °
Vậy tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là 360 ° .
Mà tổng số đo góc ngoài tại hai đỉnh B, C bằng 200 ° nên tổng số đo góc ngoài tại hai đỉnh A, D bằng 360 ° - 200 ° = 160 °
CM
5 tháng 10 2017
Đáp án cần chọn là: A
Xét tứ giác ABCD có A ^ + B ^ + C ^ + D ^ = 360 ° (định lí)
Hay 50 ° + B ^ + 150 ° + 45 ° = 360 °
⇒ B ^ = 360 ° - 50 ° - 150 ° - 45 ° = 115 °
Nên góc ngoài tại đỉnh B có số đo là 180 ° - B ^ = 180 ° - 115 ° = 65 °
CM
9 tháng 5 2017
Đáp án cần chọn là: C
C D x ^ là góc ngoài đỉnh D.
Tứ giác ABCD có: D ^ = 360 ° - A ^ + B ^ + C ^ = 360 ° - 65 ° + 117 ° + 71 ° = 107 °
Vì A D C ^ và C D x ^ là hai góc kề bù nên
C D x ^ = 180 ° - D ^ = 180 ° - 107 ° = 73 °
1 tháng 11 2017
a) Có: góc ACB + góc ACx = 180 độ (kề bù)
=> góc ACB = 70 độ
Mà góc BAC + góc ABC + góc ACB = 180 độ (định lý tổng 3 góc tam giác)
=> Góc ABC = 60 độ
b) Có: góc CAy + góc BAC = 180 độ ( kề bù)
=> góc CAy = 130 độ
góc ABC + góc ABz = 180 độ (kề bù)
=> góc ABz = 120 độ
5 tháng 11 2017
Ta có: \(\widehat{C1}+\widehat{C2}=180^o\)(kề bù)
\(\widehat{C1}+110^o=180^o\)
\(\widehat{C1}=180^o-110^o=70^o\)
\(\Rightarrow\widehat{C1}=70^o\)
Xét tam giác ABC, ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(50^o+\widehat{B}+70^o=180^o\)
\(\widehat{B}=180^o-\left(50^o+70^o\right)=60^o\)
\(\Rightarrow\widehat{B}=60^o\)
Vì \(\widehat{B1}\)là số đo góc ngoài tại đỉnh A của tam giác ABC
=> \(\widehat{B1}=\widehat{A}+\widehat{C}=50^o+70^o=120^o\)
Vì \(\widehat{A1}\)là số đo góc ngoài tại đỉnh A của tam giác ABC
\(\Rightarrow\widehat{A1}=\widehat{B}+\widehat{C}=70^o+60^o=130^o\)
HP
15 tháng 6 2016
Xét hình tứ giác ABCD có:
\(A+B+C+D=360^0\) (đ/l.....)
=>\(D=360^0-\left(A+B+C\right)=360^0-\left(65^0+117^0+71^0\right)=107^0\)
=>số đo góc ngoài ở đỉnh D là : 1800-1070=730
C
2
DM
28 tháng 7 2021
Số đo góc D là: 360o - 65o - 117o - 68o = 110o
Số đo góc ngoài đỉnh D: 180o - 110o = 70o
29 tháng 7 2021
Số đo góc ngoài tại đỉnh D là:
\(180^0-\left(360^0-65^0-117^0-68^0\right)=70^0\)
15 tháng 12 2021
\(a,\widehat{C}=180^0-\widehat{A}-\widehat{B}=75^0\\ b,=180^0-\widehat{C}=105^0\\ c,\text{Đề trùng câu b}\)
15 tháng 12 2021
a) Xét tam giác ABC có:
\(\widehat{BAC}\) \(\text{+}\) \(\widehat{ABC}\) \(\text{+}\) \(\widehat{ACB}\) \(=180^o\) (Tổng 3 góc trong tam giác).
Thay số: \(60^o+45^o+\) \(\widehat{ACB}\) \(=180^o\).
\(\Rightarrow\) \(\widehat{ACB}\) \(=75^o.\)
b) Số đo góc ngoài đỉnh C là:
\(180^o-\) \(\widehat{ACB}\) = \(180^o-\) \(75^o=105^o.\)
Số đo góc ngoài tại đỉnh \(D\) là: \(360^\circ - \left( {65^\circ + 100^\circ + 60^\circ } \right) = 135^\circ \)