Cho tam giác ABC có hai đường cao BH và CK. Chứng minh rằng: Tỉ số diện tích của tam giác AHK với tam giác ABC bằng cos^2 A
Mọi người giúp mình với 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TM
tuan manh
20 tháng 7 2023
Đúng(0)
Những câu hỏi liên quan
24 tháng 3 2023
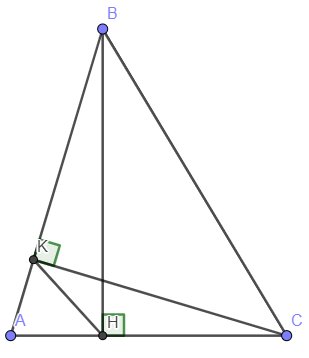
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
góc A chung
=>ΔAHB đồng dạng với ΔAKC
=>AH/AK=AB/AC
=>AH/AB=AK/AC
Vì góc BKC=góc BHC=90 độ
nên BKHC nội tiếp
=>góc AKH=góc ACB
góc KEH=góc KFH=90 độ
nên KEFH nội tiếp
=>góc AEF=góc AHK=góc ABC
=>EF//CB
20 tháng 1
a: Xét ΔKBC vuông tại K và ΔCBA vuông tại C có
\(\widehat{KBC}\) chung
Do đó: ΔKBC~ΔCBA
b:
Ta có: \(\widehat{EMC}=\widehat{BMK}\)(hai góc đối đỉnh)
\(\widehat{BMK}+\widehat{KBM}=90^0\)(ΔBKM vuông tại K)
Do đó: \(\widehat{EMC}+\widehat{KBM}=90^0\)
Ta có: \(\widehat{MEC}+\widehat{EBC}=90^0\)(ΔBCE vuông tại C)
\(\widehat{EMC}+\widehat{KBM}=90^0\)
mà \(\widehat{EBC}=\widehat{KBM}\)
nên \(\widehat{EMC}=\widehat{MEC}\)
=>ΔEMC cân tại C
4 tháng 2 2021
a) Xét ΔBHC vuông tại H và ΔCKB vuông tại K có
CB chung
\(\widehat{BCH}=\widehat{CBK}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBHC=ΔCKB(cạnh huyền-góc nhọn)
b) Ta có: ΔBHC=ΔCKB(cmt)
nên HC=KB(hai cạnh tương ứng)
Ta có: AK+KB=AB(K nằm giữa A và B)
AH+HC=AC(H nằm giữa A và C)
mà AB=AC(ΔABC cân tại A)
và KB=HC(cmt)
nên AK=AH
Xét ΔAKH có AK=AH(cmt)
nên ΔAKH cân tại A(Định nghĩa tam giác cân)
c) Ta có: ΔAKH cân tại A(cmt)
nên \(\widehat{AKH}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAKH cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AKH}=\widehat{ABC}\)
mà \(\widehat{AKH}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên HK//BC(Dấu hiệu nhận biết hai đường thẳng song song)
d) Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK(cạnh huyền-góc nhọn)
nên \(\widehat{ABH}=\widehat{ACK}\)(hai góc tương ứng)
hay \(\widehat{KBO}=\widehat{HCO}\)
Xét ΔKBO vuông tại K và ΔHCO vuông tại H có
KB=HC(cmt)
\(\widehat{KBO}=\widehat{HCO}\)(cmt)
Do đó: ΔKBO=ΔHCO(cạnh góc vuông-góc nhọn kề)
nên OB=OC(hai cạnh tương ứng)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(cmt)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: MB=MC(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(5)
Từ (3), (4) và (5) suy ra A,O,M thẳng hàng(đpcm)