Tìm nghiệm nguyên \(3x^2+5y^2=2015\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nhận xét: 345 và 5y^2 chia hết cho 5 nên 3x^2 chia hết cho 5 => x^2 chia hết cho 5 mà 3x^2 < 345 => x^2 < 345 : 3 = 115
=> x^2 = 25; 100 => y2 = 54 hoặc 9
=> chọn x^2 = 100 và y^2 = 9
=> x = 10 ; -10
y = 3; -3


Mình chưa học phương trình nên giải theo cách của lớp dưới thôi :)))
Vì \(\hept{\begin{cases}345⋮5\\5y^2⋮5\end{cases}}\Rightarrow3x^2⋮5\)
Mà \(\left(3;5\right)=1\Rightarrow x^2⋮5\Rightarrow x⋮5\)
Lại có \(3x^2\le345\Rightarrow x^2\le115\Rightarrow\left|x\right|\le10\)
Mà \(x⋮5\Rightarrow x\in\left\{0;\pm5;\pm10\right\}\)
- \(x=0\Rightarrow y^2=\frac{345}{5}=69\)không phải số chính phương
- \(x=\pm5\Rightarrow3.25+5y^2=345\)
\(\Rightarrow y^2=\frac{345-3.25}{5}=54\)không phải số chính phương
- \(x=\pm10\Rightarrow3.100+5.y^2=345\)
\(\Rightarrow y^2=\frac{345-3.100}{5}=9\Rightarrow y=\pm3\)
Vậy \(\left(x;y\right)\in\left\{\left(10;3\right);\left(10;-3\right);\left(-10;3\right);\left(-10;-3\right)\right\}\)
\(3x^2+5y^2=345=>x^2=\frac{345-5y^2}{3}=>x=\sqrt{\frac{345-5y^2}{3}}\)
MODE 7 (TABLE) nhập \(f\left(x\right)=\sqrt{\frac{345-5X^2}{3}}\)
start -9 end: 9 ,step=1
tìm đc \(\left(x;y\right)=\left(10;3\right);\left(3;10\right);\left(-10;-3\right);\left(-3;-10\right)\)
đây là sử dụng máy tính casio

Ta có:
x2 + 2y2 + 3xy + 3x + 5y = 15
<=> x2 + 2y2 + 3xy + 3x + 5y + 2 = 17
<=> (x2 + xy + 2x) + (2xy + 2y2 + 4y) + (x + y + 2) = 17
<=> (x + y + 2)(x + 2y + 1) = 17
=> (x + y + 2, x + 2y + 1) = (1,17; 17,1; - 1,-17; -17,-1)
Giải ra là tìm được x,y nhé

a)
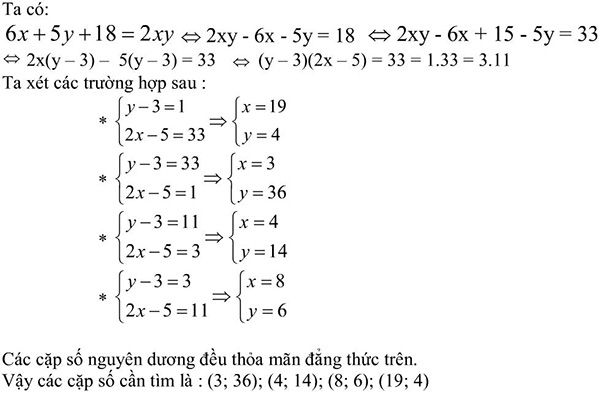
b)
Nhận thấy: x phải là số lẻ. Vì nếu x là số chẵn thì 3x^2 sẽ là số chẵn => 3x^2-4y^2 là số chẵn trong khi 13 là số lẻ
x là số lẻ => x có dạng x= 2k+1 với k thuộc Z
thay x=2k+1 vào phương trình ta có:
3(4k^2+4k+1) - 4y^2 = 13
<=> 6k^2+6k-2y^2=5
<=> 6k(k+1) = 5+2y^2
Dễ thấy vế trái là số chẵn trong khi vế phải là số lẻ => phương trình không có nghiệm nguyên => dpcm



từ nha
r lm cho
tích cho anh anh trả lời cho anh học lớp 9 rùi