Hài 4 (3,5 điểm) Cho đường tròn tâm (O) đường kính AB. I là trung điểm OA. Qua E vẽ dây CD vuông góc với AB, K là trung điểm của BC.
a) chứng minh CIOK nội tiếp đường tròn
b) Chứng minh IC.ID=IA.IB
c) Chứng minh ba điểm DOK thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔOCB có OB=OC(=R)
nên ΔOCB cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOCB cân tại O(cmt)
mà OE là đường trung tuyến ứng với cạnh BC(E là trung điểm của BC)
nên OE là đường cao ứng với cạnh BC(Định lí tam giác cân)
⇔OE⊥BC tại E
Xét tứ giác CMOE có
\(\widehat{CMO}\) và \(\widehat{CEO}\) là hai góc đối
\(\widehat{CMO}+\widehat{CEO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: CMOE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Bạn xem lại đề, sao lại có 2 điểm M trong hình vậy bạn?

Bạn xem lại đề, hình như O,M,C,D có C,M,D thẳng hàng mà

câu c hình như bn nhầm đỉnh tứ giác thì phải
d) bn cm ED là phân giác góc AEB (giống câu a) rồi dùng t/c phân giác trog và ngoài của tg AEB nhé

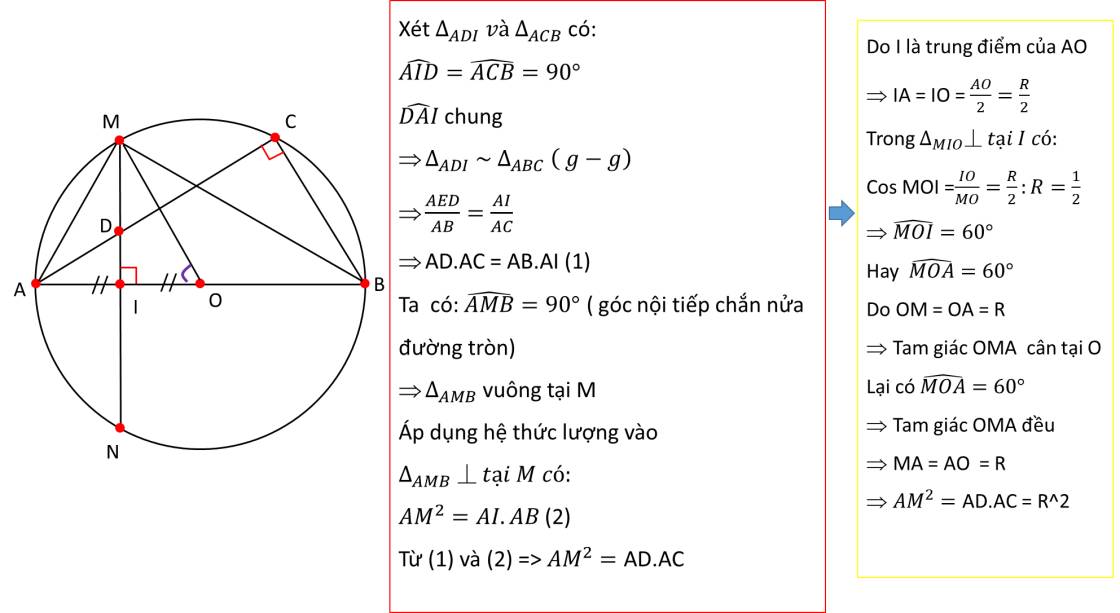
a: ΔOBC cân tại O
mà OK là trung tuyến
nênOK vuông góc BC
góc CIO+góc CKO=180 độ
=>CIOK nội tiếp
b: Xét ΔICB vuông tại I và ΔIAD vuông tại I có
góc ICB=góc IAD
=>ΔICB đồng dạng với ΔIAD
=>IC/IA=IB/ID
=>IC*ID=IA*IB