cho pt x2- 2 ( m+1)x+4m=0 .Tìm m sao cho (x1+m) (x2+m) = 3m2 + 12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
1
NT
21 tháng 4 2016
CHÀO BẠN
Áp dụng Viét
- x1*x2=4m (1)
- x1+x2=2(m+1) (2)
(*) (x1+m)(x2+m)=3m^2+12
<=>x1*x2+m(x1+x2)=3m^2+12 (**)
thay (1);(2) vô (**) =>....
Mình bày hướng có chỗ nào sai tự sửa
LA
0
BL
1
Y
1 tháng 4 2023
\(x^2+2\left(m+1\right)+4m-4=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-2\left(m+1\right)\\x_1x_2=\dfrac{c}{a}=4m-4\end{matrix}\right.\)
Ta có :
\(x_1^2+x_2^2+3x_1x_2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+3x_1x_2=0\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+x_1x_2=0\)
\(\Leftrightarrow\left[-2\left(m+1\right)\right]^2+\left(4m-4\right)=0\)
\(\Leftrightarrow4\left(m^2+2m+1\right)+4m-4=0\)
\(\Leftrightarrow4m^2+8m+4+4m-4=0\)
\(\Leftrightarrow4m^2+12m=0\)
\(\Leftrightarrow4m\left(m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-3\end{matrix}\right.\)
HK
1
22 tháng 4 2023
Thay x=5 vào pt, ta được:
25-10(m+1)+m^2-4m+5=0
=>m^2-4m+30-10m-10=0
=>m^2-14m+20=0
=>\(m=7\pm\sqrt{29}\)
x1+x2=(2m+2)
=>x2+5=16+2 căn 29 hoặc x2+5=16-2 căn 29
=>x2=11+2căn 29 hoặc x2=11-2 căn 29
EC
1
QH
1
5 tháng 4 2021
1) Thay m=1 vào phương trình, ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)
hay x=1
Vậy: Khi m=1 thì phương trình có nghiệm duy nhất là x=1
5 tháng 4 2021
1) Bạn tự làm
2) Ta có: \(\Delta'=\left(m-1\right)^2\ge0\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm
Theo Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=2m-1\end{matrix}\right.\)
a) Ta có: \(x_1+x_2=-1\) \(\Rightarrow2m=-1\) \(\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy ...
b) Ta có: \(x_1^2+x_2^2=13\) \(\Rightarrow\left(x_1+x_2\right)^2-2x_1x_2=13\)
\(\Rightarrow4m^2-4m-11=0\) \(\Leftrightarrow m=\dfrac{1\pm\sqrt{13}}{2}\)
Vậy ...
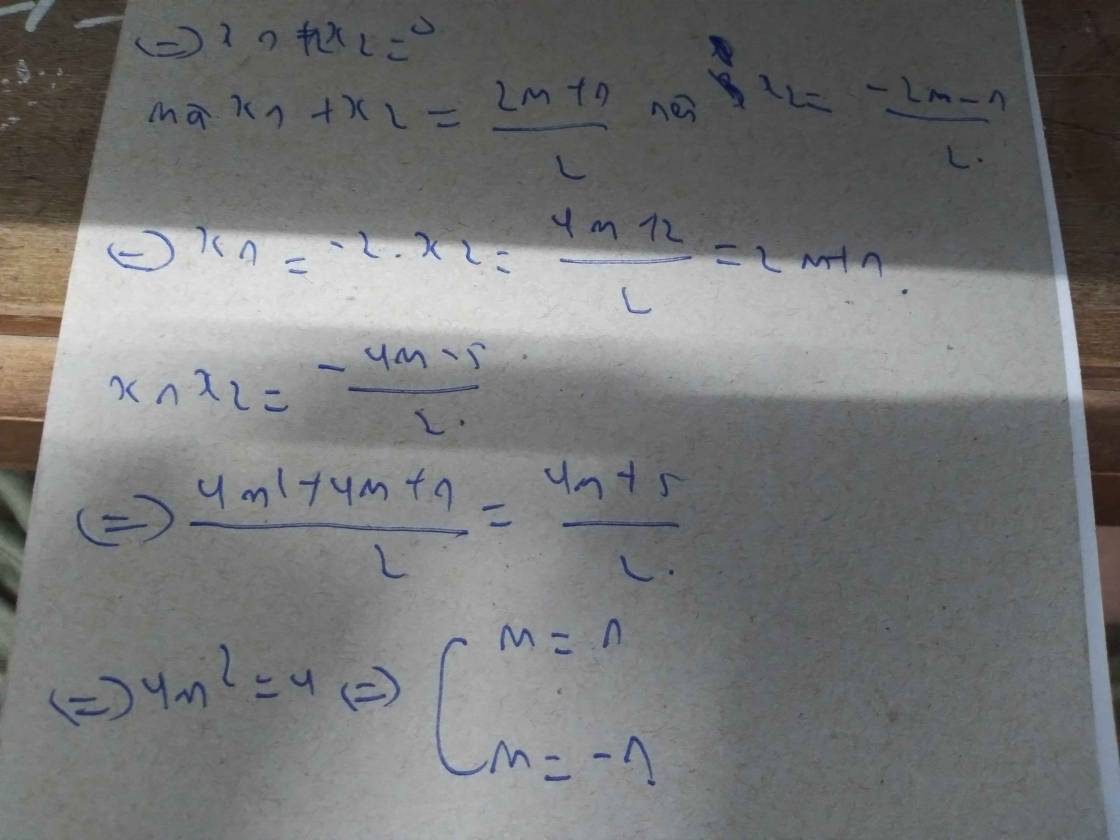
Lời giải:
Để pt có 2 nghiệm $x_1,x_2$ thì $\Delta'=(m+1)^2-4m\geq 0$
$\Leftrightarrow (m-1)^2\geq 0$
$\Leftrightarrow m\neq 1$
Khi đó, áp dụng định lý Viet:
$x_1+x_2=2(m+1)$
$x_1x_2=4m$
Khi đó:
$(x_1+m)(x_2+m)=3m^2+12$
$\Leftrightarrow x_1x_2+m(x_1+x_2)+m^2=3m^2+12$
$\Leftrightarrow 4m+2m(m+1)+m^2=3m^2+12$
$\Leftrightarrow 3m^2+6m=3m^2+12$
$\Leftrightarrow 6m=12$
$\Leftrightarrow m=2$ (tm)