Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

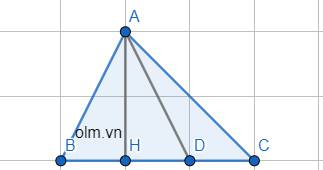
Vì AH \(\perp\) BC \(\equiv\) H nên:
BH là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB < AC => BH < HC ( Mối quan hệ đường xiên và hình chiếu )
\(\widehat{BAH}\) Đối diện cạnh BH
\(\widehat{HAC}\) Đối diện cạnh HC
mà BH < HC ( chứng minh trên)
=> \(\widehat{BAH}\) < \(\widehat{HAC}\) ( mối quan hệ giữa cạnh và góc trong tam giác)
Ta có : HD = HB (gt) (1)
AH \(\perp\) BD \(\equiv\) H (2)
Từ (1) và (2) ta có : \(\Delta\) ABD cân tại A vì AH vừa là đường cao vừa là đường trung tuyến của \(\Delta\) ABD

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc EDB=góc ECB

sửa lại đề :
Cho tam giác abc nhọn (AB<AC). Kẻ các đường cao BD, CE cắt nhau tại H.
CM: a) Tam giác ABD đồng dạng tam giác ACE
b) tam giác AEH đồng dạng tam giác CEB
a,Xét \(\Delta ABD\)và \(\Delta ACE\)có :
\(\widehat{ADB}=\widehat{AEC}=90^0\)
\(\widehat{BAC}\)chung
\(\Rightarrow\Delta ABD~\Delta ACE\left(g.g\right)\)

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED

Xét ΔABD vuông tại D và ΔCHD vuông tại D có
góc BAD=góc HCD
=>ΔABD đồng dạng vớiΔCHD
1/ Ta có:
• Góc AHB bằng 90 độ (vì AD là đường cao của tam giác ABD).
• Góc AEB bằng góc AFB bằng 90 độ (vì AB là đường cao của tam giác AFB và AC là đường cao của tam giác AEC).
Góc AHE bằng góc AFE (vì đường cao AH đồng quy với đường chéo EF của tứ giác AHEF).
• Góc AHP bằng góc AKP bằng 90 độ (vì KA là đường đường kính của đường tròn (O)).
• Góc AEP bằng góc AFP (vì đường cao AE đồng quy với đường chéo AF của tứ giác AEPF).
Do đó, ta có thể kết luận rằng 5 điểm P, A, E, H, F nằm trên cùng một đường tròn. Để xác định tâm T của đường tròn này, ta lấy hai đường kính của đường tròn là AP và EF, sau đó kẻ đường thẳng qua giữa chúng. Đường thẳng này cắt đường tròn tại T, là tâm của đường tròn.
2/ Ta có:
• Góc AHE bằng góc AFE (vì đường cao AH đồng quy với đường chéo EF của tứ giác AHEF).
• Góc EHF bằng 90 độ (vì EF là đường cao của tam giác EHF).
o Góc FHE bằng góc FEM (vì đường cao FH đồng quy với đường chéo EM của tứ giác FHEM).
Do đó, ta có thể kết luận rằng EM và FM là hai tiếp tuyến của đường tròn (T).
3/ Ta cần chứng minh rằng tam giác DEF nội tiếp đường tròn (M). Ta có:
• Góc EHF bằng 90 độ (vì EF là đường cao của tam giác EHF).
• Góc FEM bằng góc FHE (vì đường cao FH đồng quy với đường chéo EM của tứ giác FHEM). • Góc FHE bằng góc DAE