...
Đọc tiếp
(1+11.3)(1+12.4)(1+13.5)...(1+12019+2021)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 3 2022
uses crt;
var a:real;
i,n:integer;
begin
clrscr;
readln(n);
a:=0;
for i:=1 to n do
a:=a+1/(i*(i+2));
writeln(a:4:2);
readln;
end.
PT
1
CM
13 tháng 8 2017
Đáp án là A
l i m 1 1 . 3 + 1 2 . 4 + . . . + 1 n n + 2
Ta có :
l i m 1 1 . 3 + 1 2 . 4 + . . . + 1 n n + 2 = l i m 2 1 . 3 + 2 2 . 4 + . . . + 2 n n + 2
l i m 1 2 1 - 1 3 + 1 2 - 1 4 + 1 3 - 1 5 . . . + 1 n - 1 n + 2 = l i m 1 2 1 + 1 2 - 1 n + 2 = 3 4
CM
4 tháng 9 2019
Đáp án A
Ta có: 0 < u n < 1 1.2 + 1 2.3 + ... + 1 n n + 1 = 1 − 1 n + 1 < 1
Dãy u n bị chặn.
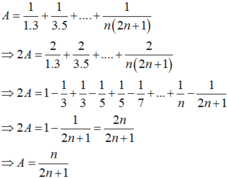
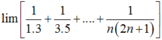
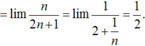
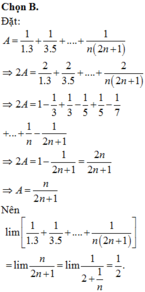
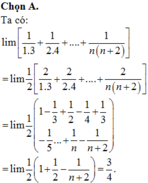
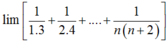
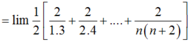
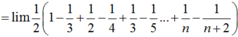
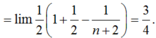
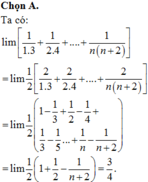
\(\left(1+\dfrac{1}{1\cdot3}\right)\left(1+\dfrac{1}{2\cdot4}\right)\left(1+\dfrac{1}{3\cdot5}\right)\cdot...\cdot\left(1+\dfrac{1}{2019\cdot2021}\right)\)
\(=\left(1+\dfrac{1}{2^2-1}\right)\left(1+\dfrac{1}{3^2-1}\right)\cdot...\cdot\left(1+\dfrac{1}{2020^2-1}\right)\)
\(=\dfrac{2^2}{\left(2-1\right)\left(2+1\right)}\cdot\dfrac{3^2}{\left(3-1\right)\left(3+1\right)}\cdot...\cdot\dfrac{2020^2}{\left(2020-1\right)\left(2020+1\right)}\)
\(=\dfrac{2}{1}\cdot\dfrac{3}{2}\cdot...\cdot\dfrac{2020}{2019}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2020}{2021}\)
\(=2020\cdot\dfrac{2}{2021}=\dfrac{4040}{2021}\)