
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

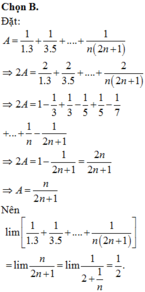

a) \(\lim \frac{{5n + 1}}{{2n}} = \lim \frac{{5 + \frac{1}{n}}}{2} = \frac{{5 + 0}}{2} = \frac{5}{2}\)
b) \(\lim \frac{{6{n^2} + 8n + 1}}{{5{n^2} + 3}} = \lim \frac{{6 + \frac{8}{n} + \frac{1}{{{n^2}}}}}{{5 + \frac{3}{{{n^2}}}}} = \frac{{6 + 0 + 0}}{{5 + 0}} = \frac{6}{5}\)
c) \(\lim \frac{{\sqrt {{n^2} + 5n + 3} }}{{6n + 2}} = \lim \frac{{\sqrt {1 + \frac{5}{n} + \frac{3}{{{n^2}}}} }}{{6 + \frac{2}{n}}} = \frac{{\sqrt {1 + 0 + 0} }}{{6 + 0}} = \frac{1}{6}\)
d) \(\lim \left( {2 - \frac{1}{{{3^n}}}} \right) = \lim 2 - \lim {\left( {\frac{1}{3}} \right)^n} = 2 - 0 = 0\)
e) \(\lim \frac{{{3^n} + {2^n}}}{{{{4.3}^n}}} = \lim \frac{{1 + {{\left( {\frac{2}{3}} \right)}^n}}}{4} = \frac{{1 + 0}}{4} = \frac{1}{4}\)
g) \(\lim \frac{{2 + \frac{1}{n}}}{{{3^n}}}\)
Ta có \(\lim \left( {2 + \frac{1}{n}} \right) = \lim 2 + \lim \frac{1}{n} = 2 + 0 = 2 > 0;\lim {3^n} = + \infty \Rightarrow \lim \frac{{2 + \frac{1}{n}}}{{{3^n}}} = 0\)

a) \(\lim \frac{{2{n^2} + 6n + 1}}{{8{n^2} + 5}} = \lim \frac{{{n^2}\left( {2 + \frac{6}{n} + \frac{1}{{{n^2}}}} \right)}}{{{n^2}\left( {8 + \frac{5}{{{n^2}}}} \right)}} = \lim \frac{{2 + \frac{6}{n} + \frac{1}{n}}}{{8 + \frac{5}{n}}} = \frac{2}{8} = \frac{1}{4}\)
b) \(\lim \frac{{4{n^2} - 3n + 1}}{{ - 3{n^3} + 6{n^2} - 2}} = \lim \frac{{{n^3}\left( {\frac{4}{n} - \frac{3}{{{n^2}}} + \frac{1}{{{n^3}}}} \right)}}{{{n^3}\left( { - 3 + \frac{6}{n} - \frac{2}{{{n^3}}}} \right)}} = \lim \frac{{\frac{4}{n} - \frac{3}{{{n^2}}} + \frac{1}{{{n^3}}}}}{{ - 3 + \frac{6}{n} - \frac{2}{{{n^3}}}}} = \frac{{0 - 0 + 0}}{{ - 3 + 0 - 0}} = 0\).
c) \(\lim \frac{{\sqrt {4{n^2} - n + 3} }}{{8n - 5}} = \lim \frac{{n\sqrt {4 - \frac{1}{n} + \frac{3}{{{n^2}}}} }}{{n\left( {8 - \frac{5}{n}} \right)}} = \frac{{\sqrt {4 - 0 + 0} }}{{8 - 0}} = \frac{2}{8} = \frac{1}{4}\).
d) \(\lim \left( {4 - \frac{{{2^{{\rm{n}} + 1}}}}{{{3^{\rm{n}}}}}} \right) = \lim \left( {4 - 2 \cdot {{\left( {\frac{2}{3}} \right)}^{\rm{n}}}} \right) = 4 - 2.0 = 4\).
e) \(\lim \frac{{{{4.5}^{\rm{n}}} + {2^{{\rm{n}} + 2}}}}{{{{6.5}^{\rm{n}}}}} = \lim \frac{{{{4.5}^{\rm{n}}} + {2^2}{{.2}^{\rm{n}}}}}{{{{6.5}^{\rm{n}}}}} = \lim \frac{{{5^n}.\left[ {4 + 4.{{\left( {\frac{2}{5}} \right)}^{\rm{n}}}} \right]}}{{{{6.5}^n}}} = \lim \frac{{4 + 4.{{\left( {\frac{2}{5}} \right)}^{\rm{n}}}}}{6} = \frac{{4 + 4.0}}{6} = \frac{2}{3}\).
g) \(\lim \frac{{2 + \frac{4}{{{n^3}}}}}{{{6^{\rm{n}}}}} = \lim \left( {2 + \frac{4}{{{{\rm{n}}^3}}}} \right).\lim {\left( {\frac{1}{6}} \right)^{\rm{n}}} = \left( {2 + 0} \right).0 = 0\).

\(a=\lim n\left(\sqrt[3]{-1+\dfrac{2}{n}-\dfrac{5}{n^3}}\right)=+\infty.\left(-1\right)=-\infty\)
\(b=\lim\left(\sqrt{n+1}+\sqrt{n}\right)=+\infty\)
\(c=\lim n\left(\dfrac{1}{n^2+n}-1\right)=+\infty.\left(-1\right)=-\infty\)
\(d=\lim\left(\dfrac{2n^2-1-2n\left(n+1\right)}{n+1}\right)=\lim\left(\dfrac{-1-2n}{n+1}\right)=-2\)
\(e=\lim\dfrac{2n^2+n-3+\dfrac{1}{n}}{\dfrac{2}{n}-3}=\dfrac{+\infty}{-3}=-\infty\)

\(a=lim\dfrac{\left(\dfrac{2}{6}\right)^n+1-\dfrac{1}{4}\left(\dfrac{4}{6}\right)^n}{\left(\dfrac{3}{6}\right)^n+6}=\dfrac{1}{6}\)
\(b=\lim\dfrac{\left(n+1\right)^2}{3n^2+4}=\lim\dfrac{n^2+2n+1}{3n^2+4}=\lim\dfrac{1+\dfrac{2}{n}+\dfrac{1}{n^2}}{3+\dfrac{4}{n^2}}=\dfrac{1}{3}\)
\(c=\lim\dfrac{n\left(n+1\right)}{2\left(n^2-3\right)}=\lim\dfrac{n^2+n}{2n^2-6}=\lim\dfrac{1+\dfrac{1}{n}}{2-\dfrac{6}{n^2}}=\dfrac{1}{2}\)
\(d=\lim\left[1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}\right]=\lim\left[1-\dfrac{1}{n+1}\right]=1\)
\(e=\lim\dfrac{1}{2}\left[1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2n-1}-\dfrac{1}{2n+1}\right]\)
\(=\lim\dfrac{1}{2}\left[1-\dfrac{1}{2n+1}\right]=\dfrac{1}{2}\)

Chụp ảnh hoặc sử dụng gõ công thức nhé bạn. Để vầy khó hiểu lắm


Đề bị lỗi công thức rồi bạn. Bạn cần viết lại để được hỗ trợ tốt hơn.

a/ Bạn coi lại đề bài, 3n^2 +n^2 thì bằng 4n^2 luôn chứ ko ai cho đề bài như vậy cả
b/ \(\lim\limits\dfrac{\dfrac{n^3}{n^3}+\dfrac{3n}{n^3}+\dfrac{1}{n^3}}{-\dfrac{n^3}{n^3}+\dfrac{2n}{n^3}}=-1\)
c/ \(=\lim\limits\dfrac{-\dfrac{2n^3}{n^2}+\dfrac{3n}{n^2}+\dfrac{1}{n^2}}{-\dfrac{n^2}{n^2}+\dfrac{n}{n^2}}=\lim\limits\dfrac{-2n}{-1}=+\infty\)
d/ \(=\lim\limits\left[n\left(1+1\right)\right]=+\infty\)
e/ \(\lim\limits\left[2^n\left(\dfrac{2n}{2^n}-3+\dfrac{1}{2^n}\right)\right]=\lim\limits\left(-3.2^n\right)=-\infty\)
f/ \(=\lim\limits\dfrac{4n^2-n-4n^2}{\sqrt{4n^2-n}+2n}=\lim\limits\dfrac{-\dfrac{n}{n}}{\sqrt{\dfrac{4n^2}{n^2}-\dfrac{n}{n^2}}+\dfrac{2n}{n}}=-\dfrac{1}{2+2}=-\dfrac{1}{4}\)
g/ \(=\lim\limits\dfrac{n^2+3n-1-n^2}{\sqrt{n^2+3n-1}+n}+\lim\limits\dfrac{n^3-n^3+n}{\sqrt[3]{\left(n^3-n\right)^2}+n.\sqrt[3]{n^3-n}+n^2}\)
\(=\lim\limits\dfrac{\dfrac{3n}{n}-\dfrac{1}{n}}{\sqrt{\dfrac{n^2}{n^2}+\dfrac{3n}{n^2}-\dfrac{1}{n^2}}+\dfrac{n}{n}}+\lim\limits\dfrac{\dfrac{n}{n^2}}{\dfrac{\sqrt[3]{\left(n^3-n\right)^2}}{n^2}+\dfrac{n\sqrt[3]{n^3-n}}{n^2}+\dfrac{n^2}{n^2}}\)
\(=\dfrac{3}{2}+0=\dfrac{3}{2}\)

a: \(\lim\limits\dfrac{5n+1}{2n}=\lim\limits\dfrac{\dfrac{5n}{n}+\dfrac{1}{n}}{\dfrac{2n}{n}}=\lim\limits\dfrac{5+\dfrac{1}{n}}{2}=\dfrac{5+0}{2}=\dfrac{5}{2}\)
b: \(\lim\limits\dfrac{6n^2+8n+1}{5n^2+3}\)
\(=\lim\limits\dfrac{\dfrac{6n^2}{n^2}+\dfrac{8n}{n^2}+\dfrac{1}{n^2}}{\dfrac{5n^2}{n^2}+\dfrac{3}{n^2}}\)
\(=\lim\limits\dfrac{6+\dfrac{8}{n}+\dfrac{1}{n^2}}{5+\dfrac{3}{n^2}}\)
\(=\dfrac{6+0+0}{5+0}=\dfrac{6}{5}\)
c: \(\lim\limits\dfrac{3^n+2^n}{4\cdot3^n}\)
\(=\lim\limits\dfrac{\dfrac{3^n}{3^n}+\left(\dfrac{2}{3}\right)^n}{4\cdot\left(\dfrac{3^n}{3^n}\right)}\)
\(=\lim\limits\dfrac{1+\left(\dfrac{2}{3}\right)^n}{4}=\dfrac{1+0}{4}=\dfrac{1}{4}\)
d: \(\lim\limits\dfrac{\sqrt{n^2+5n+3}}{6n+2}\)
\(=\lim\limits\dfrac{\sqrt{\dfrac{n^2}{n^2}+\dfrac{5n}{n^2}+\dfrac{3}{n^2}}}{\dfrac{6n}{n}+\dfrac{2}{n}}\)
\(=\lim\limits\dfrac{\sqrt{1+\dfrac{5}{n}+\dfrac{3}{n^2}}}{6+\dfrac{2}{n}}\)
\(=\dfrac{\sqrt{1+0+0}}{6}=\dfrac{1}{6}\)
\(a,lim\dfrac{5n+1}{2n}=lim\dfrac{\dfrac{5n}{n}+\dfrac{1}{n}}{\dfrac{2n}{n}}=lim\dfrac{5+\dfrac{1}{n}}{2}=\dfrac{5}{2}\\ b,lim\dfrac{6n^2+8n+1}{5n^2+3}=lim\dfrac{\dfrac{6n^2}{n^2}+\dfrac{8n}{n^2}+\dfrac{1}{n^2}}{\dfrac{5n^2}{n^2}+\dfrac{3}{n^2}}=lim\dfrac{6+\dfrac{8}{n}+\dfrac{1}{n^2}}{5+\dfrac{3}{n^2}}=\dfrac{6}{5}\)
\(c,lim\dfrac{3^n+2^n}{4.3^n}=\dfrac{\dfrac{3^n}{3^n}+\dfrac{2^n}{3^n}}{\dfrac{4.3^n}{3^n}}=\dfrac{1+\left(\dfrac{2}{3}\right)^n}{4}=\dfrac{1}{4}\)
\(d,lim\dfrac{\sqrt{n^2+5n+3}}{6n+2}=lim\dfrac{\sqrt{\dfrac{n^2+5n+3}{n^2}}}{\dfrac{6n}{n}+\dfrac{2}{n}}=lim\dfrac{\sqrt{1+\dfrac{5}{n}+\dfrac{3}{n^2}}}{6+\dfrac{2}{n}}=\dfrac{1}{6}\)

\(a=\lim4^n\left(1-\left(\dfrac{3}{4}\right)^n\right)=+\infty.1=+\infty\)
\(b=\lim\left(4^n+2.2^n+1-4^n\right)=\lim2^n\left(2+\dfrac{1}{2^n}\right)=+\infty.2=+\infty\)
\(c=limn^3\left(\sqrt{\dfrac{2}{n}-\dfrac{3}{n^4}+\dfrac{11}{n^6}}-1\right)=+\infty.\left(-1\right)=-\infty\)
\(d=\lim n\left(\sqrt{2+\dfrac{1}{n^2}}-\sqrt{3-\dfrac{1}{n^2}}\right)=+\infty\left(\sqrt{2}-\sqrt{3}\right)=-\infty\)
\(e=\lim\dfrac{3n\sqrt{n}+1}{\sqrt{n^2+3n\sqrt{n}+1}+n}=\lim\dfrac{3\sqrt{n}+\dfrac{1}{n}}{\sqrt{1+\dfrac{3}{\sqrt{n}}+\dfrac{1}{n^2}}+1}=\dfrac{+\infty}{2}=+\infty\)