Mọi người giải hộ mình bài 10 với bài 11 trong hình với

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải chi tiết
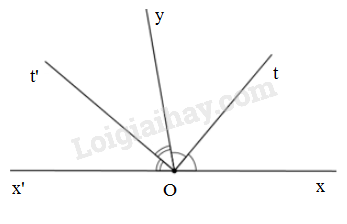
Hai góc xOyxOy và x′Oyx′Oy là hai góc kề bù nên ˆxOy+ˆx′Oy=1800xOy^+x′Oy^=1800 mà ˆxOy=1000xOy^=1000 nên ˆx′Oy=1800−ˆxOyx′Oy^=1800−xOy^=1800−1000=800=1800−1000=800
Vì OtOt là tia phân giác của góc xOyxOy nên ˆxOt=ˆtOy=ˆxOy2xOt^=tOy^=xOy^2=10002=500=10002=500
Vì Ot′Ot′ là tia phân giác của góc x′Oyx′Oy nên ˆx′Ot′=ˆt′Oyx′Ot′^=t′Oy^=ˆx′Oy2=8002=400=x′Oy^2=8002=400
+ Góc x′Otx′Ot và góc xOtxOt là hai góc kề bù nên ˆx′Ot+ˆxOt=1800x′Ot^+xOt^=1800
Suy ra ˆx′Ot=1800−ˆxOt=1800−500=1300x′Ot^=1800−xOt^=1800−500=1300
+ Góc xOt′xOt′ và góc x′Ot′x′Ot′ là hai góc kề bù nên ˆxOt′+ˆx′Ot′=1800xOt′^+x′Ot′^=1800
Suy ra ˆxOt′=1800−ˆx′Ot′=1800−400=1400xOt′^=1800−x′Ot′^=1800−400=1400
+ Vì tia Ot′Ot′ nằm giữa hai tia Ox′Ox′ và Oy,Oy, tia OtOt nằm giữa hai tia OxOx và OyOy
Lại có hai góc xOyxOy và x′Oyx′Oy là hai góc kề bù nên tia OyOy nằm giữa hai tia OxOx và Ox′Ox′
Suy ra tia OyOy nằm giữa hai tia OtOt và Ot′Ot′
Do đó ˆyOt′+ˆyOt=ˆt′OtyOt′^+yOt^=t′Ot^
Suy ra ˆt′Ot=500+400=900t′Ot^=500+400=900

\(=\dfrac{10}{17}-\dfrac{5}{3}+7-\dfrac{8}{13}+\dfrac{11}{25}\)
\(=\dfrac{30}{51}-\dfrac{85}{51}+\dfrac{175}{25}+\dfrac{11}{25}-\dfrac{8}{13}\)
\(=\dfrac{-55}{51}+\dfrac{186}{25}-\dfrac{8}{13}\)
\(=\dfrac{-55\cdot325+186\cdot663-8\cdot1275}{16575}=\dfrac{95243}{16575}\)


Đặt \(m=a^2,n=b^2\)
Ta đưa bài toán về dạng tìm GTLN và GTNN của \(A=m-3mn+2n\)
Khi đó ta suy ra từ giả thiết :
\(\left(m+n+1\right)^2+3mn+1=4m+5n\)
\(\Rightarrow m-3mn+2n=\left(m+n+1\right)^2+1-3m-3n\)
\(=\left(m^2+n^2+2mn+2m+2n+1\right)+1-3n-3m\)
\(=m^2+n^2+2mn-m-n+2\)
\(=m^2+m\left(2n-1\right)+n^2-n+2\)
\(=m^2+m\left(2n-1\right)+\frac{\left(2n-1\right)^2}{4}+\frac{7}{4}\)
\(=\left(m+\frac{2n-1}{2}\right)^2+\frac{7}{4}\ge\frac{7}{4}\)
Hay \(A\ge\frac{7}{4}\) . Đẳng thức xảy ra khi \(m=\frac{1-2n}{2}\)
Tới đây bạn tự suy ra nhé ^^

bài 10 : X x 10= 1,643+7,357 410-X= 91,08 : 3,6
X x 10 = 9 410-X=25,3
X = 9 : 10 X=410-25,3
X = 0,9 X = 384,7