Cho tam giác ABC có tia phân giác của góc ABC cắt cạnh AC ở D, tia phân giác của góc ACB cắt cạnh AB ở E. Biết BE + CD = BC. Tính số đo góc BAC?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 2 2018
Câu hỏi của Nguyễn Duy Thịnh - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 2 2018
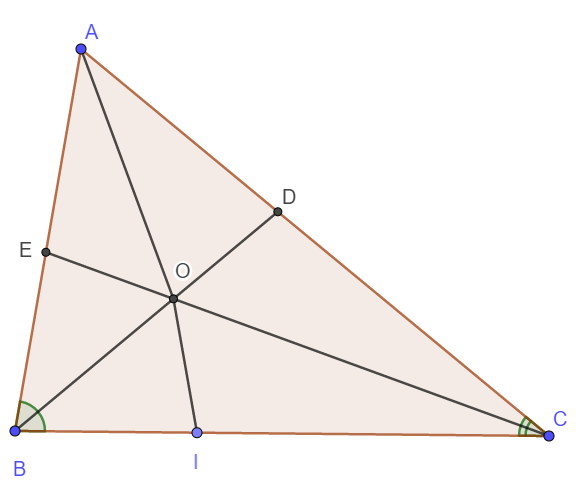
Trên BC lấy điểm I sao cho BI = BE.
Do BC = BE + DC nên IC = DC.
Ta có : \(\Delta EOB=\Delta IOB\left(c-g-c\right)\Rightarrow\widehat{EOB}=\widehat{IOB}\)
\(\Delta DOC=\Delta IOC\left(c-g-c\right)\Rightarrow\widehat{DOC}=\widehat{IOC}\)
Mà \(\widehat{EOB}=\widehat{DOC}\Rightarrow\widehat{EOB}=\widehat{IOB}=\widehat{DOC}=\widehat{IOC}\)
Vậy thì \(\widehat{IOB}=\widehat{DOC}=\widehat{IOC}=\frac{180^o}{3}=60^o\)
\(\Rightarrow\widehat{BOC}=60^o+60^o=120^o\)
\(\Rightarrow\frac{\widehat{B}}{2}+\frac{\widehat{C}}{2}=180^o-120^o=60^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=120^o\Rightarrow\widehat{A}=60^o\)
19 tháng 1 2018
có A = 60 độ (gt)
suy ra c+b=180-60=120
mà c1=1/2 c:b1=1/2 b ( tích chất tia phân giác )
suy ra c1+b1=120:2=60
suy ra BOC = 180-60=120
B)
xét Tam giác BOE và BOF bằng nhau theo ( cạnh góc cạnh)
suy ra OB là tia phân giác ủa EOF
C: có Phân giác Ce và BD cắt Nhau tại O
mà AF cắt CE và BD tại O suy ra AF LÀ phân giác của góc BAC
từ đó suy ra OD=OE=OF ( tích chất của tia phân giác )
, hình thì m tự vẽ bố éo rảnh ngồi vẽ :))
CH
Cô Hoàng Huyền
Admin
VIP
19 tháng 1 2018
a) Ta có \(\widehat{B_1}=\widehat{B_2};\widehat{C_1}=\widehat{C_2}\Rightarrow\widehat{B_1}+\widehat{C_1}=\frac{\widehat{B}+\widehat{C}}{2}=\frac{180^o-\widehat{A}}{2}=\frac{180^o-60^o}{2}=60^o\)
Vậy thì \(\widehat{BOC}=180^o-60^o=120^o\)
b) Xét tam giác BEO và BFO có:
BE = BF (gt)
BO chung
\(\widehat{B_1}=\widehat{B_2}\)
\(\Rightarrow\Delta BEO=\Delta BFO\left(c-g-c\right)\)
\(\Rightarrow\widehat{BOE}=\widehat{BOF}\) (Hai góc tương ứng)
Vậy OB là tia phân giác góc EOF.
c) Gọi K, H là chân đường cao hạ từ O xuống AB và AC
Do O là giao điểm của 3 đường phân giác nên OH = OK
Ta có \(\widehat{EAD}+\widehat{EOD}=60^o+\widehat{BOC}=60^o+120^o=180^o\)
\(\Rightarrow\widehat{AEO}+\widehat{ODK}=180^o\Rightarrow\widehat{OEH}=\widehat{ODK}\Rightarrow\widehat{HOE}=\widehat{KOD}\)
Vậy thì \(\Delta OEH=\Delta ODK\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow OE=OD\)
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 2 2018
Câu hỏi của Nguyễn Duy Thịnh - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 2 2018
Câu hỏi của Nguyễn Duy Thịnh - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
30 tháng 1 2022
a: Xét tứ giác BEDF có
DF//BE
ED//BF
Do đó: BEDF là hình bình hành
mà BD là đường phân giác
nên BEDF là hình thoi
Suy ra: DB là tia phân giác của góc EDF
b: Ta có: ED//BC
nên \(\widehat{AED}=\widehat{ABC};\widehat{ADE}=\widehat{ACB}\)