cho hình chữ nhật ABCD có AB=2a, BC=a 0<a thuộc R . Tính theo a diện tích xung quanh của hình trụ tạo thành khi quanh hình chữ nhật ABCD quanh đường thẳng AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


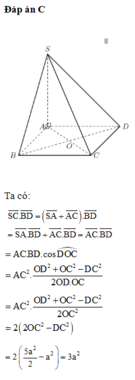
Đáp án C
Ta có: S C → . B D → = S A → + A C → . B D → = S A → . B D → + A C → . B D → = A C → . B D →
= A C . B D . cos D O C ^ = A C 2 . O D 2 + O C 2 − D C 2 2 O D . O C
= A C 2 . O D 2 + O C 2 − D C 2 2 O C 2 = 2 2 O C 2 − D C 2
= 2 5 a 2 2 − a 2 = 3 a 2
Do đó: cos S C → , B D → = S C → . B D → S C . B D = 3 a 2 3 a . a 5 = 1 5
Vậy cos S C , B D = cos S C → , B D → = 1 5


Đáp án B
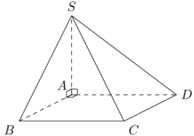
Diện tích đáy ABCD là SABCD = AB. BC = a.2a = 2a2.
Thể tích khối chóp S.ABCD là:
V = 1 3 . S A . S A B C D = 1 3 . 2 a . 2 a 2 = 4 a 3 3

\(\left|\overrightarrow{AB}-\overrightarrow{BC}\right|=\left|\overrightarrow{AB}+\overrightarrow{CB}\right|=BD=a\sqrt{6}\)

Đề bài thiếu độ dài SD hoặc dữ kiện để tính độ dài SD nên ko thể tính được góc giữa SA và (ABCD)

ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường và AC=BD
=>O là trung điểm chung của AC và BD
ABCD là hình chữ nhật
=>AB=CD=2a; BC=AD
O là trung điểm của AC
=>\(AC=2\cdot AO=2a\cdot\sqrt{5}\)
=>\(BD=2a\sqrt{5}\)
ABCD là hình chữ nhật
=>ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC^2=AC^2-AB^2=\left(2a\sqrt{5}\right)^2-\left(2a\right)^2=20a^2-4a^2=16a^2\)
=>BC=4a
=>\(\left|\overrightarrow{BC}\right|=4a\)

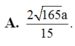
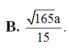

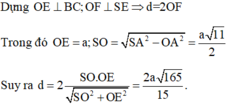
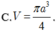

Khi quay hình chữ nhật ABCD quanh đường AB thì được hình trụ có
R=BC=a, h=AB=2a
\(S_{XQ}=2\cdot pi\cdot a\cdot2a=4\cdot pi\cdot a^2\)