Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D.
Hướng dẫn giải:
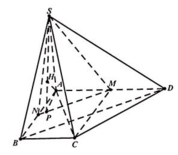
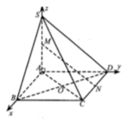
O = A C ∩ B D , Gọi , I là trung điểm cạnh đáy BC.
Vì SA = SB = SC = SD nên S O ⊥ ( A B C D )
Từ đó ta chứng mình được B C ⊥ ( S O I )
⇒ O H ⊥ ( S B C ) (với O H ⊥ B C tại SI).
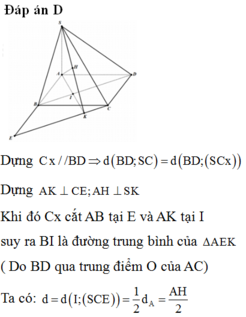
Do E F / / ( S B C ) S K ⊂ ( S B C )
nên d(EF,SK) = d(EF,(SBC)) = OH.
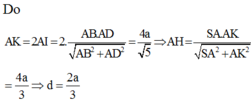
Thực hiện tính toàn để được
O C = 1 2 A C = a 5 2 ⇒ S O = a 3 2
Kết luận:


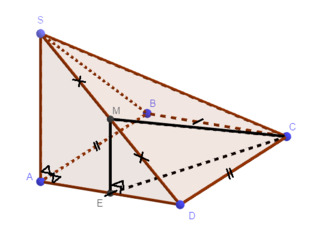
Gọi E là trung điểm AD, ta có: ME//SA (ME là đường trung bình tam giác SAD) và SA, CE chéo nhau; suy ra (MCE) vuông góc (ABCD) và không chứa SA; suy ra SA//(MCE). Suy ra, d(SA,CM) = d(SA,(MCE)) = d(A,(MCE)) = d(D,(MCE)) = d(D,EC) = ED.DC/EC = a.3a/a\(\sqrt{10}\) = 3a\(\sqrt{10}\)/10.
Xin lỗi, mình sửa lại bài giải.
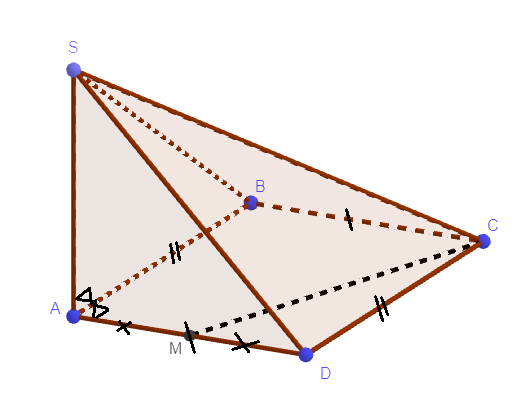
d(SA,CM) = d(A,CM) = d(D,CM) = MD.DC/CM = a.3a/a\(\sqrt{10}\) = 3a\(\sqrt{10}\)/10.
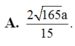
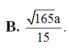
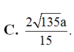
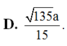
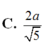
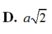
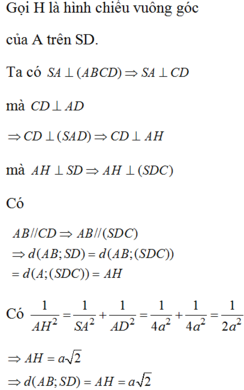
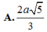
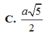

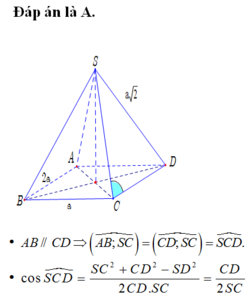
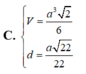
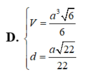
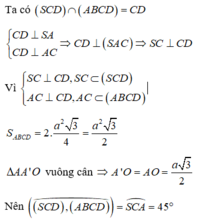
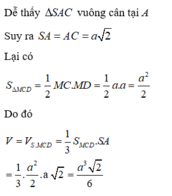
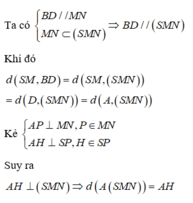

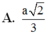
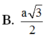
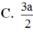
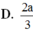
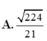
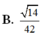
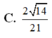
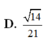
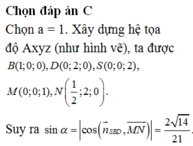


Đáp án A.