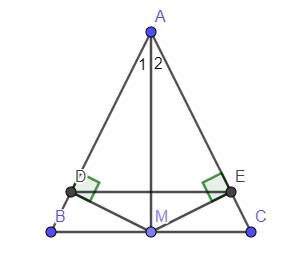
Cho tam giác ABC cân tại A, AM là trung tuyến.
a) c/m tam giác ABM= tam giác ACM
b) Kẻ MD vuông góc AB, ME vuông góc AC. C/m MD= ME
c) Kẻ BH vuông góc AC. Gọi I là giao điểm của BH và MD. C/m tam giác BIM cân.
d) Gọi O là giao điểm của AM và BH. Kẻ ON vuông góc AB. C/m C, O, N thẳng hàng.