Tìm x
22x + 4x + 2 = 272
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HG
12 tháng 12 2016
D=5x2+5x-27x+27/(x)22(x)(2) +22
D=5x(x+1)-27(x+1)/(x-2)2
D=(5x-27)(x+1)/(x-20(x-2)
12 tháng 12 2016
bai cua ban Hakawa Genzo sai roi -27x+27 e thanh -27(x-1) ma
9 tháng 11 2021
\(1,\Rightarrow3^{x-3}=\left(3^2\right)^8:\left(3^3\right)^5=3^{16}:3^{15}=3^1\\ \Rightarrow x-3=1\\ \Rightarrow x=4\\ 2,\Rightarrow7^x\left(1+7^2\right)=350\\ \Rightarrow7^x=\dfrac{350}{50}=7=7^1\\ \Rightarrow x=1\)
9 tháng 11 2021
\(3,\Rightarrow2^{2+2x+2}-2^{2x}=240\\ \Rightarrow2^{2x}\left(2^4-1\right)=240\\ \Rightarrow2^{2x}=\dfrac{240}{15}=16=2^4\\ \Rightarrow2x=4\Rightarrow x=2\)
TT
0
CM
17 tháng 8 2017
Cách 1. Lập bảng xét dấu.
Cách 2. f(x) không xác định khi x = 2 và 2 ∈ ((-3)/2; +∞) nên A sai. Dễ thấy x = (-7)/4 thì x 2 – 4 < 0; x – 2 < 0; 2x + 3 < 0 ⇒ f(x) < 0, vì vậy C và D sai.
Đáp án: B
2D
1
AH
Akai Haruma
Giáo viên
26 tháng 12 2022
Lời giải:
Ta có:
\(C=\frac{5(x^2-4x+4)-2x+5}{x^2-4x+4}=\frac{5(x-2)^2-2(x-2)+1}{(x-2)^2}=5-\frac{2}{x-2}+\frac{1}{(x-2)^2}\)
Đặt $\frac{1}{x-2}=t$ thì:
$C=t^2-2t+5=(t-1)^2+4\geq 4$ với mọi $t$
$\Rightarrow C_{\min}=4$. Vậy GTNN của $C$ là $4$. Giá trị này đạt tại $t=1$
$\Leftrightarrow \frac{1}{x-2}=1\Leftrightarrow x=3$
12 tháng 8 2021
d) \(4x^4-x^2=x^2\left(4x^2-1\right)=x^2\left(2x-1\right)\left(2x+1\right)\)
e) Ta có: \(6x^2-7x-5\)
\(=6x^2-10x+3x-5\)
\(=2x\left(3x-5\right)+\left(3x-5\right)\)
\(=\left(3x-5\right)\left(2x+1\right)\)
f: Ta có: \(-4x^2+23x-15\)
\(=-4x^2+20x+3x-15\)
\(=-4x\left(x-5\right)+3\left(x-5\right)\)
\(=\left(x-5\right)\left(-4x+3\right)\)
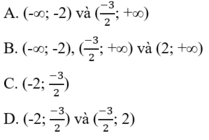
\(2^{2x}+4^{x+2}=272\)
\(\Rightarrow4^x+4^x\cdot4^2=272\)
\(\Rightarrow4^x\left(1+4^2\right)=272\)
\(\Rightarrow4^x\cdot17=272\)
\(\Rightarrow4^x=16\)
\(4^x=4^2\)
\(\Rightarrow x=2\)
thiếu dấu \(\Rightarrow\) rồi bạn