Chứng minh rằng:A=36/1x3x5+36/3x5x7+36/5x7x9+....+36/25x27x29
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 3 2018
2A=\(\frac{2}{1.2.3}\)+\(\frac{2}{2.3.4}\)+...+\(\frac{2}{18.19.20}\)
=1/1.2-1/2.3+1/2.3-1/3.4+...+1/18.19-1/19.20
=1/2-1/19.20
A=1/4-1/19.20.2
vậy A<1/4
MT
0
NC
3
TQ
7
24 tháng 5 2016
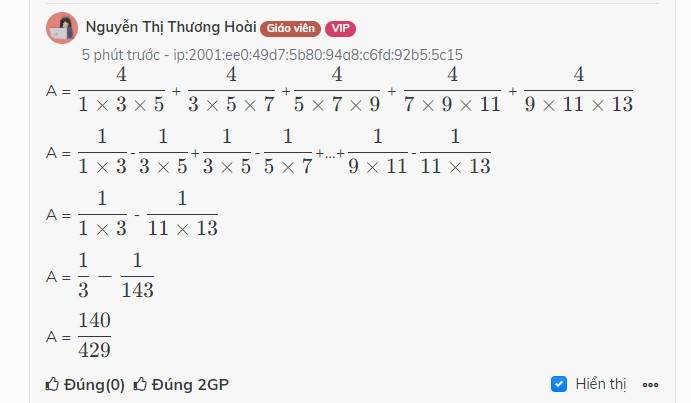
\(\frac{4}{1x3x5}+\frac{4}{3x5x7}+...+\frac{4}{9x11x13}\)
\(=\frac{1}{1x3}-\frac{1}{3x5}+\frac{1}{3x5}-...+\frac{1}{9x11}-\frac{1}{11x13}\)
\(=\frac{1}{3}-\frac{1}{143}\)
\(=\frac{140}{429}\)
HL
1
OY
12 tháng 8 2021
\(\dfrac{4}{1\times3\times5}+\dfrac{4}{3\times5\times7}+\dfrac{4}{5\times7\times9}+\dfrac{4}{7\times9\times11}\)
=\(\dfrac{5-1}{1\times3\times5}+\dfrac{7-3}{3\times5\times7}+\dfrac{9-5}{5\times7\times9}+\dfrac{11-7}{7\times9\times11}\)
=\(\dfrac{1}{1\times3}-\dfrac{1}{3\times5}+\dfrac{1}{3\times5}-\dfrac{1}{5\times7}+...+\dfrac{1}{9\times11}-\dfrac{1}{11\times13}\)
=\(\dfrac{1}{3}-\dfrac{1}{143}=\dfrac{140}{429}\)
DN
2
\(A=9\left(\dfrac{4}{1\cdot3\cdot5}+\dfrac{4}{3\cdot5\cdot7}+...+\dfrac{4}{25\cdot27\cdot29}\right)\)
\(=9\left(\dfrac{1}{1\cdot3}-\dfrac{1}{3\cdot5}+\dfrac{1}{3\cdot5}-\dfrac{1}{5\cdot7}+...+\dfrac{1}{25\cdot27}-\dfrac{1}{27\cdot29}\right)\)
\(=9\left(\dfrac{1}{3}-\dfrac{1}{783}\right)=\dfrac{260}{87}\)