Cho đường thẳng y = x2. Tìm điểm A thuộc parabol sao cho tiếp tuyến với parabol tại A song song với đường thẳng y = 4x+5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi phương trình tiếp tuyến d tại A của parabol có dạng \(y=4x+b\) (\(b\ne5\))
Pt hoành độ giao điểm d và (P):
\(x^2=4x+b\Leftrightarrow x^2-4x-b=0\) (1)
d tiếp xúc (P) \(\Leftrightarrow\) (1) có nghiệm kép
\(\Leftrightarrow\Delta'=4+b=0\Rightarrow b=-4\)
Hoành độ giao điểm: \(x=\frac{4}{2.1}=2\Rightarrow y=4\Rightarrow A\left(2;4\right)\)

Gọi tiếp tuyến tại A có dạng \(y=ax+b\Rightarrow a=2\Rightarrow y=2x+b\)
Phương trình hoành độ giao điểm:
\(x^2=2x+b\Leftrightarrow x^2-2x-b=0\)
\(\Delta'=1+b=0\Rightarrow b=-1\Rightarrow y=2x-1\)
Khi đó hoành độ A là nghiệm \(x^2=2x-1\Leftrightarrow x=1\Rightarrow y=1\)
Vậy \(A\left(1;1\right)\)

Tiếp tuyến với (P) tại A có dạng:(d) y=ax+b
Vì (d) song song với y=4x+5 nên: a=4
=>y=4x+b
Phương trình hoành độ giao điểm của (P) và (d) là:
x2=4x+b
<=>x2-4x-b=0
Vì (d) là tiếp tuyến của (P) nên:
\(\Delta=0\),PT có 2 nghiệm kép: \(x_1=x_2=2\)
=>y=4
Vậy A(1;4)
Tiếp tuyến với (P) tại A có dạng:(d) y=ax+b
Vì (d) song song với y=4x+5 nên: a=4
=>y=4x+b
Phương trình hoành độ giao điểm của (P) và (d) là:
x2=4x+b
<=>x2-4x-b=0
Vì (d) là tiếp tuyến của (P) nên:
Δ=0Δ=0,PT có 2 nghiệm kép: x1=x2=2x1=x2=2
=>y=4
Vậy A(1;4)

- Ta có
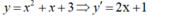
- Giả sử M ( x 0 , y 0 ) là tiếp điểm của tiếp tuyến với parabol y = x 2 + x + 3 .
- Vì tiếp tuyến song song với đường thẳng d: y = 4 3 - x ( đường thẳng này có hệ số góc bằng -1).
- Nên:
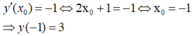
- Phương trình tiếp tuyến là:
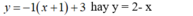
Chọn C.

Vì (d1)//(d) nên \(\left\{{}\begin{matrix}a=3\\b\ne-4\end{matrix}\right.\)
Vậy: (d1): y=3x+b
Thay x=-2 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)
Thay x=-2 và y=2 vào (d1), ta được:
\(3\cdot\left(-2\right)+b=2\)
\(\Leftrightarrow b=8\)(thỏa ĐK)
Vậy: (d1): y=3x+8
để \(\left(d1\right)\) sogn song với \(\left(d\right)\)
\(< =>\left\{{}\begin{matrix}a=3\\b\ne-4\end{matrix}\right.\)
để (d1) cắt (P) tại A có hoành độ -2\(=>x=-2\)
\(=>\dfrac{1}{2}x^2=3x+b< =>\dfrac{1}{2}\left(-2\right)^2=3\left(-2\right)+b=>b=8\left(tm\right)\)
=>\(\left(d1\right):y=3x+8\)

Ta có y = x 2 + x + 3 ⇒ y ' = 2 x + 1
Giả sử M x 0 ; y 0 là tiếp điểm của tiếp tuyến với parabol y = x 2 + x + 3
Vì tiếp tuyến song song với đường thẳng y = 4 3 − x nên y ' ( x 0 ) = − 1 ⇔ 2 x 0 + 1 = − 1 ⇔ x 0 = − 1 ; y ( − 1 ) = 3
Phương trình tiếp tuyến là y = − 1 x + 1 + 3 hay y = 2 − x
Chọn đáp án C