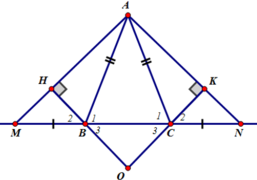
Cho tam giác ABC cân tại A. Trên tia đối tia BA và tia CA lấy điểm M và N
sao cho BM = CN. Chứng minh: NM + BC < 2BN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TH
Thầy Hùng Olm
Manager
VIP
24 tháng 2 2023
Đúng(1)
Những câu hỏi liên quan
25 tháng 1 2020
Hình bạn tự vẽ nha :))
a)* Ta có: \(\Delta ABC\)cân tại A <=> AB=AC
\(\hept{\begin{cases}AM=AB+MB\\AN=AC+NC\end{cases}\Rightarrow AM=AN}\)(do \(AB=AC;MB=NC\))
\(\Rightarrow\Delta AMN\)cân tại A
* Từ \(\Delta ABC\)cân tại A, có: \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\)(1)
Từ \(\Delta AMN\)cân tại A, có: \(\widehat{AMN}=\frac{180^o-\widehat{A}}{2}\)(2)
Từ (1) và (2), suy ra: \(\widehat{ABC}=\widehat{AMN}\)
\(\Rightarrow MN//BC\)(2 góc đồng vị bằng nhau)
b) Xét \(\Delta ABI\)và \(\Delta ACI\)có:
\(\hept{\begin{cases}AB=AC\\AIchung\\IB=IC\end{cases}\Rightarrow\Delta ABI=\Delta}ACI\left(ccc\right)\)
\(\Rightarrow\widehat{BAI}=\widehat{CAI}\)(2 góc tương ứng)
\(\Rightarrow AI\)là p/giác của \(B\widehat{A}C\) (3)
Tương tự, ta có: \(\widehat{MAE}=\widehat{NAE}\)
\(\Rightarrow AE\)là p/ giác của \(\widehat{BAC}\)(4)
Từ (3) và (4), ta có: A,I,E thẳng hàng
9 tháng 1 2022
Xét ΔBAM và ΔCAN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
DO dó: ΔBAM=ΔCAN
Suy ra: AM=AN
hay ΔAMN cân tại A
Bn tham khảo nhé!
CM
16 tháng 2 2017
ΔABC cân tại A suy ra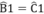 
Ta lại có :
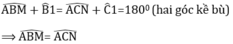
- ΔABM và ΔACN có
AB = AC (Do ΔABC cân tại A).
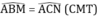
BM = CN(gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (hai cạnh tương ứng) ⇒ ΔAMN cân tại A.
HL
27 tháng 2 2015
Từ đỉnh A kẻ đường cao AH (H thuộc BC) (1)
Ta có : tam giác ABC cân tại A (gt) (2)
Từ(1) và(2)=> HB=HC(=1/2 BC) (3)
Lại có: BM=CN (gt) (4)
M nằm trên tia đối của tia BC, N nằm trên tia đối của tia CB => M,B,C.N thẳng hàng (5)
Từ (3)và (4)=>HB+BM=HC+CN (6)
Từ (5) và (6)=>AH vừa là đường cao, vừa là đường trung tuyến trong tam giác AMN
=> Tam giác AMN cân tại A (đpcm)
UF
12 tháng 8 2015
Nếu BAC = 60 độ với tam giác ABC cân nữa thì thành tam giác đều rồi?
Đâu có AB > BC được?