CM pt sau vô nghiệm : /x-2/=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MT
0
TN
9 tháng 1 2017
\(2x^2-6x+7=0\)
\(\Rightarrow2x^2-6x+\frac{9}{2}+\frac{5}{2}=0\)
\(\Rightarrow2\left(x^2-3x+\frac{9}{4}\right)+\frac{5}{2}=0\)
\(\Rightarrow2\left(x-\frac{3}{2}\right)^2+\frac{5}{2}>0\)( vô nghiệm)
23 tháng 6 2018
b1 \(\frac{x+a}{x+1}+\frac{x-2}{x}=2\)
ĐKXĐ \(\hept{\begin{cases}x\ne0\\x\ne-1\end{cases}}\)
\(\Leftrightarrow x\left(x+a\right)+\left(x-2\right)\left(x+1\right)=2x\left(x+1\right)\)
\(\Leftrightarrow x^2+ax+x^2-x-2=2x^2+2x\)
\(\Leftrightarrow ax-3x=2\)
\(\Leftrightarrow\left(a-3\right)x=2\)
để pt vô nghiệm thì a-3=0 <=>a=3 thì pt vô nghiệm
2,\(4x-k+4=kx+k\)
\(\Leftrightarrow4x-kx=2k-4\)
\(\Leftrightarrow\left(4-k\right)x=2k-4\)
để pt có nghiệm duy nhất thì 4-k khác 0 <=> k khác 4 thì pt có nghiệm duy nhất là\(\frac{2k-4}{4-k}\)
pt vô nghiệm thì 4-k=0 <=.>k=4
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 7 2021
a.
Khi \(m=2\) pt trở thành:
\(2x+3=0\Rightarrow x=-\dfrac{3}{2}\)
b.
Để pt có nghiệm \(x=-1\)
\(\Rightarrow\left(m^2-m\right).\left(-1\right)+m^2-1=0\)
\(\Leftrightarrow-m^2+m+m^2-1=0\)
\(\Leftrightarrow m-1=0\)
\(\Leftrightarrow m=1\)
c.
Pt tương đương:
\(\left(m^2-m\right)x=-\left(m^2-1\right)\)
\(\Leftrightarrow m\left(m-1\right)x=-\left(m-1\right)\left(m+1\right)\)
Pt vô nghiệm khi:
\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\-\left(m-1\right)\left(m+1\right)\ne0\end{matrix}\right.\) \(\Leftrightarrow m=0\)
\(\Rightarrow\) pt có nghiệm khi \(m\ne0\)
Pt có vô số nghiệm khi:
\(\left\{{}\begin{matrix}m\left(m-1\right)=0\\-\left(m-1\right)\left(m+1\right)=0\end{matrix}\right.\) \(\Leftrightarrow m=1\)
AH
Akai Haruma
Giáo viên
5 tháng 7 2021
Lời giải:
a. Khi $m=2$ thì pt trở thành:
$2x+3=0\Leftrightarrow x=-\frac{3}{2}$
b. Để pt có nghiệm $x=-1$ thì:
$(m^2-m).(-1)+m^2-1=0$
$\Leftrightarrow m-1=0\Leftrightarrow m=1$
c.
PT $\Leftrightarrow (m^2-m)x=1-m^2$
Để pt vô nghiệm thì: \(\left\{\begin{matrix} m^2-m=0\\ 1-m^2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m(m-1)=0\\ (1-m)(1+m)\neq 0\end{matrix}\right.\)
\(\Leftrightarrow m=0\)
PT có vô số nghiệm khi \(\left\{\begin{matrix} m^2-m=0\\ 1-m^2= 0\end{matrix}\right.\Leftrightarrow m=1\)
Để PT có nghiệm thì: $m\neq 0$
8 tháng 1 2021
a) 2(x+1)=3.2x
<=> 2x + 2 = 3 + 2x
<=> 2x - 2x = 3-2
<=> 0x = 1 => pt vô nghiệm.
b)2(1-1,5x)+3x=0
<=> 2 - 3x = -3x
<=> 2 = -3x + 3x => pt vô nghiệm.
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2021
\(mx-m+2nx-n-x=2\)
\(\Leftrightarrow\left(m+2n-1\right)x=m+n+2\)
Pt đã cho có vô số nghiệm khi và chỉ khi:
\(\left\{{}\begin{matrix}m+2n-1=0\\m+n+2=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}n=3\\m=-5\end{matrix}\right.\)
11 tháng 9 2023
a: \(\left\{{}\begin{matrix}ax+y=2a\\x-a=1-ay\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}ax+y=2a\\x+ay=a+1\end{matrix}\right.\)
Khi a=2 thì hệ sẽ là \(\left\{{}\begin{matrix}2x+y=4\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=4\\2x+4y=6\end{matrix}\right.\)
=>-3y=-2 và x+2y=3
=>y=2/3 và x=3-2y=3-4/3=5/3
2:
a: Để hệ có 1 nghiệm duy nhất thì \(\dfrac{a}{1}< >\dfrac{1}{a}\)
=>a^2<>1
=>a<>1 và a<>-1
Để hệ có vô số nghiệm thì \(\dfrac{a}{1}=\dfrac{1}{a}=\dfrac{2a}{a+1}\)
=>a^2=1 và a^2+a=2a
=>a=1
Để hệ vô nghiệm thì \(\dfrac{a}{1}=\dfrac{1}{a}< >\dfrac{2a}{a+1}\)
=>a^2=1 và a^2+a<>2a
=>a=-1
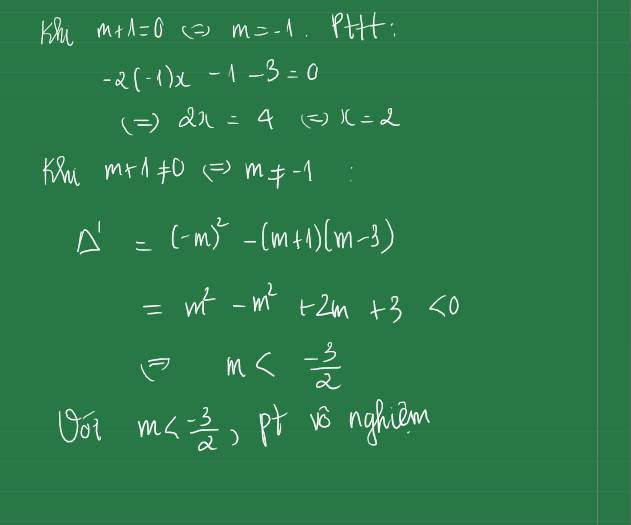
Phương trình này có nghiệm nha bạn