Cho các số dương a,b thỏa mãn:ab+a+b=3
Tìm GTNN của biểu thức: \(a^2+b^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TD
1
12 tháng 8 2023
Ta có:
P = a + b + c ≤ a + b + a + b = 2(a + b) ≤ 2(-1) = -2
Ta cũng có:
P = a + b + c ≤ a + b + c - 2abc ≥ a + b + c - 2(-1)(-1)(-1) = -3
Vậy GTNN của P = -3 và GTLN của P = -2.
AH
Akai Haruma
Giáo viên
2 tháng 5 2023
Lời giải:
$P=\frac{a^2b^2+b^2c^2+c^2a^2}{abc}$
Áp dụng BĐT AM-GM, dạng $(x+y+z)^2\geq 3(xy+yz+xz)$ ta có:
$(a^2b^2+b^2c^2+c^2a^2)^2\geq 3(a^2b^4c^2+a^4b^2c^2+a^2b^2c^4)$
$=3a^2b^2c^2(a^2+b^2+c^2)=3a^2b^2c^2$
$\Rightarrow a^2b^2+b^2c^2+c^2a^2\geq \sqrt{3}abc$
$\Rightarrow P=\frac{a^2b^2+b^2c^2+c^2a^2}{abc}\geq \sqrt{3}$
Vậy $P_{\min}=\sqrt{3}$. Giá trị này đạt tại $a=b=c=\frac{1}{\sqrt{3}}$
NA
1
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
Đặt \(P=\dfrac{a^3}{a^2+b^2+ab}+\dfrac{b^3}{b^2+c^2+bc}+\dfrac{c^3}{c^2+a^2+ca}\)
Ta có: \(\dfrac{a^3}{a^2+b^2+ab}=a-\dfrac{ab\left(a+b\right)}{a^2+b^2+ab}\ge a-\dfrac{ab\left(a+b\right)}{3\sqrt[3]{a^3b^3}}=a-\dfrac{a+b}{3}=\dfrac{2a-b}{3}\)
Tương tự: \(\dfrac{b^3}{b^2+c^2+bc}\ge\dfrac{2b-c}{3}\) ; \(\dfrac{c^3}{c^2+a^2+ca}\ge\dfrac{2c-a}{3}\)
Cộng vế:
\(P\ge\dfrac{a+b+c}{3}=673\)
Dấu "=" xảy ra khi \(a=b=c=673\)
CM
23 tháng 5 2017
Ta có:
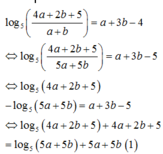
Xét hàm số
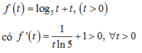
Hàm số f t đồng biến trên 0 ; + ∞
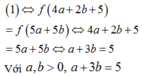
ta có:
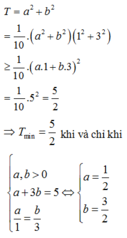
Chọn: D
CM
20 tháng 10 2017
Đáp án B
Ta có: log 5 4 a + 2 b + 5 a + b = a + 3 b − 4
⇔ log 5 4 a + 2 b + 5 + 4 a + 2 b + 5 = log 5 5 a + 5 b + 5 a + 5 b
Xét hàm số f t = log 5 t + t t > 0 ⇒ f t đồng biến trên 0 ; + ∞
Do đó f 4 a + 2 b + 5 = f 5 a + 5 b ⇔ 4 a + 2 b + 5 = 5 a + 5 b
⇔ a + 3 b = 5 ⇒ T = 5 − 3 b 2 + b 2 = 10 b 2 − 30 b + 25 = 10 b − 3 2 2 + 5 2 ≥ 5 2
CM
15 tháng 9 2019
Vì: a + 1 1 + b 2 = a + 1 − b 2 ( a + 1 ) 1 + b 2 ; 1 + b 2 ≥ 2 b n ê n a + 1 1 + b 2 ≥ a + 1 − b 2 ( a + 1 ) 2 b = a + 1 − a b + b 2
Tương tự: b + 1 1 + c 2 ≥ b + 1 − b c + c 2 ; c + 1 1 + a 2 ≥ c + 1 − c a + a 2 ⇒ M ≥ a + b + c + 3 − ( a + b + c ) + ( a b + b c + c a ) 2 = 3 + 3 − ( a b + b c + c a ) 2
Chứng minh được: 3 ( a b + b c + c a ) ≤ ( a + b + c ) 2 = 9 a c ⇒ 3 − ( a b + b c + c a ) 2 ≥ 0 ⇒ M ≥ 3
Dấu “=” xảy ra khi a = b = c = 1. Giá trị nhỏ nhất của M bằng 3.
7 tháng 6 2021
a)Có \(a^2+1\ge2a\) với mọi a; \(b^2+1\ge2b\) với mọi b
Cộng vế với vế \(\Rightarrow a^2+b^2+2\ge2\left(a+b\right)\)
Dấu = xảy ra <=> a=b=1
b) Áp dụng BĐT bunhiacopxki có:
\(\left(x+y\right)^2\le\left(1+1\right)\left(x^2+y^2\right)\Leftrightarrow\left(x+y\right)^2\le2\)
\(\Leftrightarrow-\sqrt{2}\le x+y\le\sqrt{2}\)
\(\Rightarrow\left(x+y\right)_{max}=\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=\dfrac{\sqrt{2}}{2}\)
\(\left(x+y\right)_{min}=-\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=-\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=-\dfrac{\sqrt{2}}{2}\)
c) \(S=\dfrac{1}{ab}+\dfrac{1}{a^2+b^2}=\dfrac{1}{a^2+b^2}+\dfrac{1}{2ab}+\dfrac{1}{2ab}\)
Với x,y>0, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\) (1)
Thật vậy (1) \(\Leftrightarrow\dfrac{y+x}{xy}\ge\dfrac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)\(\Leftrightarrow\left(x-y\right)^2\ge0\) (lđ)
Áp dụng (1) vào S ta được:
\(S\ge\dfrac{4}{a^2+b^2+2ab}+\dfrac{1}{2ab}\)
Lại có: \(ab\le\dfrac{\left(a+b\right)^2}{4}\) \(\Leftrightarrow2ab\le\dfrac{\left(a+b\right)^2}{2}\Leftrightarrow2ab\le\dfrac{1}{2}\)\(\Rightarrow\dfrac{1}{2ab}\ge2\)
\(\Rightarrow S\ge\dfrac{4}{\left(a+b\right)^2}+2=6\)
\(\Rightarrow S_{min}=6\Leftrightarrow a=b=\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
\(a^2+ab+b^2=\dfrac{1}{2}\left(a+b\right)^2+\dfrac{1}{2}\left(a^2+b^2\right)\ge\dfrac{1}{2}\left(a+b\right)^2+\dfrac{1}{4}\left(a+b\right)^2=\dfrac{3}{4}\left(a+b\right)^2\)
Tương tự, ta có:
\(M\ge\dfrac{\sqrt{3}}{2}\left(a+b\right)+\dfrac{\sqrt{3}}{2}\left(b+c\right)+\dfrac{\sqrt{3}}{2}\left(c+a\right)=\sqrt{3}\left(a+b+c\right)=3\sqrt{3}\)
Dấu "=" xảy ra khi \(a=b=c=1\)
9 nha ban