giải hệ phương trình : 2x+|2y-5| = 3 ; x-3|2y-5| = -2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
TN
0
PT
1
CM
11 tháng 5 2018
Lấy phương trình (2) trừ phương trình (1), vế trừ vế ta được:
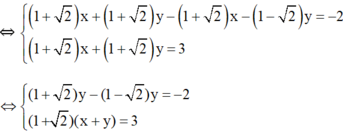
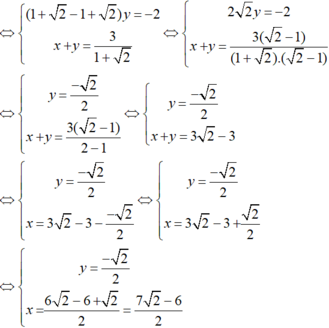
Vậy hệ phương trình có nghiệm duy nhất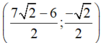 
Lưu ý:
PT
1
CM
16 tháng 2 2019
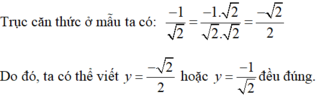
2 x - y = 5 x + y + 2 x + 2 y - 5 = 0
Ta đưa về giải hai hệ phương trình:
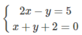
hoặc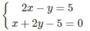 
Giải hệ:
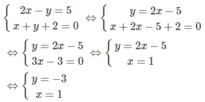
Giải hệ:
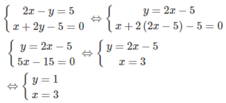
Vậy hệ phương trình đã cho có hai nghiệm
( x 1 ; y 1 ) = (1; -3) và ( x 2 ; y 2 ) = (3; 1)
11 tháng 4 2021
\(\hept{\begin{cases}2x-y=3\\3x-2y=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-4x+2y=-6\\3x-2y=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-x=-1\\2x-y=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\2.1-y=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\y=-1\end{cases}}\)
Vậy hpt có nghiệm\(\left(x;y\right)=\left(1;-1\right)\)
4 tháng 1 2022
\(\Leftrightarrow\left\{{}\begin{matrix}-2x-2y=5\\2x-2y=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4y=17\\x-y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{17}{4}\\x=6+y=\dfrac{-17}{4}+6=\dfrac{7}{4}\end{matrix}\right.\)
14 tháng 5 2021
$\begin{cases}2x+y=4\\x+2y=5\end{cases}$
`<=>` $\begin{cases}2x+y=4\\2x+4y=10\end{cases}$
`<=>` $\begin{cases}3y=6\\x=5-3y\end{cases}$
`<=>` $\begin{cases}y=2\\y=1\end{cases}$
Vậy `(x,y)=(2,1)`
14 tháng 5 2021
$\begin{cases}2x+y=4\\x+2y=5\end{cases}$
`<=>` $\begin{cases}2x+y=4\\2x+4y=10\end{cases}$
`<=>` $\begin{cases}3y=6\\x=5-2y\end{cases}$
`<=>` $\begin{cases}y=2\\y=1\end{cases}$
Vậy `(x,y)=(2,1)`
AM
20 tháng 4 2022
Có: \(\left\{{}\begin{matrix}x+2y=5\\2x-3y=-4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x+4y=10\left(1\right)\\2x-3y=-4\left(2\right)\end{matrix}\right.\)
Lấy (1) trừ (2) vế theo vế, ta có: 7y=14 hay y=2 \(\Rightarrow x=1\)
Vậy nghiệm của hệ phương trình là (1;2)
20 tháng 4 2022
\(\left\{{}\begin{matrix}x+2y=5\\2x-3y=-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x+6y=15\\4x-6y=-8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}7x=7\\x+2y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\1+2y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
CM
2 tháng 9 2017
Xét hệ phương trình 2 x − 2 y = 3 3 2 x − 6 y = 5 có 2 3 2 = − 2 − 6 ≠ 3 5 ⇔ 1 3 = 1 3 ≠ 3 5 nên hệ phương trình vô nghiệm
Đáp án: B
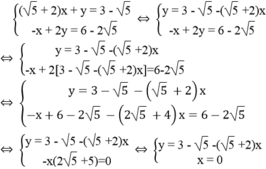
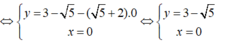
Lời giải:
$2x+|2y-5|=3$
$x-3|2y-5|=-2$
$\Rightarrow 3(2x+|2y-5|)+(x-3|2y-5|)=3.3+(-2)$
$\Leftrightarrow 7x=7$
$\Leftrightarrow x=1$
$|2y-5|=3-2x=3-2.1=1$
$\Rightarrow 2y-5=\pm 1$
$\Rightarrow y=3$ hoặc $y=2$
Vậy $(x,y)=(1,3); (1,2)$