Cho đường tròn tâm O, điểm M nằm ngoài đường tròn, vẽ các tiếp tuyến MN, MP (N,P là các tiếp điểm). a) Chứng minh rằng OM là đường trung trực của NP. b) Tính độ dài NP biết ON= 2cm, OM= 4cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
14 tháng 7 2020
Cho sửa lại đề tí ==* , câu b) là c/m MR // AO => MC // AO :>
a. Ta có: AM = AN (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AMN cân tại A
Mặt khác AO là đường phân giác của góc MAN ( tính chất hai tiếp tuyến cắt nhau )
Suy ra AO là đường cao của tam giác AMN ( tính chất tam giác cân )
Vậy \(OA\perp MN\)
b. Tam giác MNC nội tiếp trong đường tròn (O) có NC là đường kính nên góc (CMN) = 90o
Suy ra: \(NM\perp MC\)
Mà \(OA\perp MN\)(chứng minh trên)
Suy ra: OA // MC
c. Ta có: \(AN\perp NC\) (tính chất tiếp tuyến)
Áp dụng định lí Pitago vào tam giác vuông AON ta có :
AO2 = AN2 + ON2
Suy ra : AN2 = AO2 – ON2 = 52 – 32 = 16
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: \(MH=NH=\frac{MN}{2}\) (tính chất tam giác cân)
Tam giác AON vuông tại N có \(NH\perp AO\). Theo hệ thức lượng trong tam giác vuông, ta có:
OA . NH = AN . ON => \(NH=\frac{\left(AN.ON\right)}{AO}=\frac{\left(4.3\right)}{5}=2,4\)
MN = 2.NH = 2.2,4 = 4,8 (cm)
Vậy .....................
24 tháng 6 2017
a) ta có : AN = AM (tính chất tiếp tuyến)
\(\Rightarrow\) tam giác AMN cân tại A
OA là tia phân giác cũng là đường cao
\(\Rightarrow\) OA \(\perp\) MN (đpcm)
24 tháng 6 2017
b) đặc H là giao điểm của MN và AO
ta có MH = HN (OA \(\perp\) MN \(\Rightarrow\) H là trung điểm MN)
mà CO = CN = R
\(\Rightarrow\) OH là đường trung bình của tam giác MNC
\(\Rightarrow\) OH // MC \(\Leftrightarrow\) MC // OA (đpcm)
CM
10 tháng 6 2017
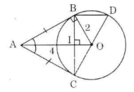
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có :
CI = IB
CO = OD (bán kính)
⇒ BD // HO (HO là đường trung bình của BCD) ⇒ BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
A C 2 = O A 2 – O C 2 = 4 2 – 2 2 = 12
=> AC = √12 = 2√3 (cm)
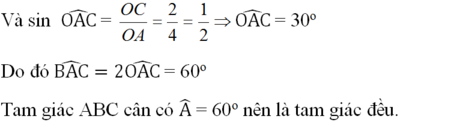
Do đó AB = BC = AC = 2√3 (cm).
7 tháng 12 2023
a: Xét (O) có
SM,SN là tiếp tuyến
Do đó: SM=SN
=>S nằm trên đường trung trực của MN(1)
Ta có: OM=ON
=>O nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra SO là đường trung trực của MN
=>SO\(\perp\)MN
b: Xét (O) có
ΔMNA nội tiếp
NA là đường kính
Do đó: ΔMNA vuông tại M
Xét ΔAMN vuông tại M có AN là cạnh huyền
nên AN là cạnh lớn nhất trong ΔAMN
=>AN>MN
c: Ta có: OS\(\perp\)MN
MN\(\perp\)MA
Do đó: OS//MA
d: Gọi giao điểm của MN và OS là H
OS là đường trung trực của MN
=>OS\(\perp\)NM tại trung điểm của NM
=>OS\(\perp\)NM tại H và H là trung điểm của MN
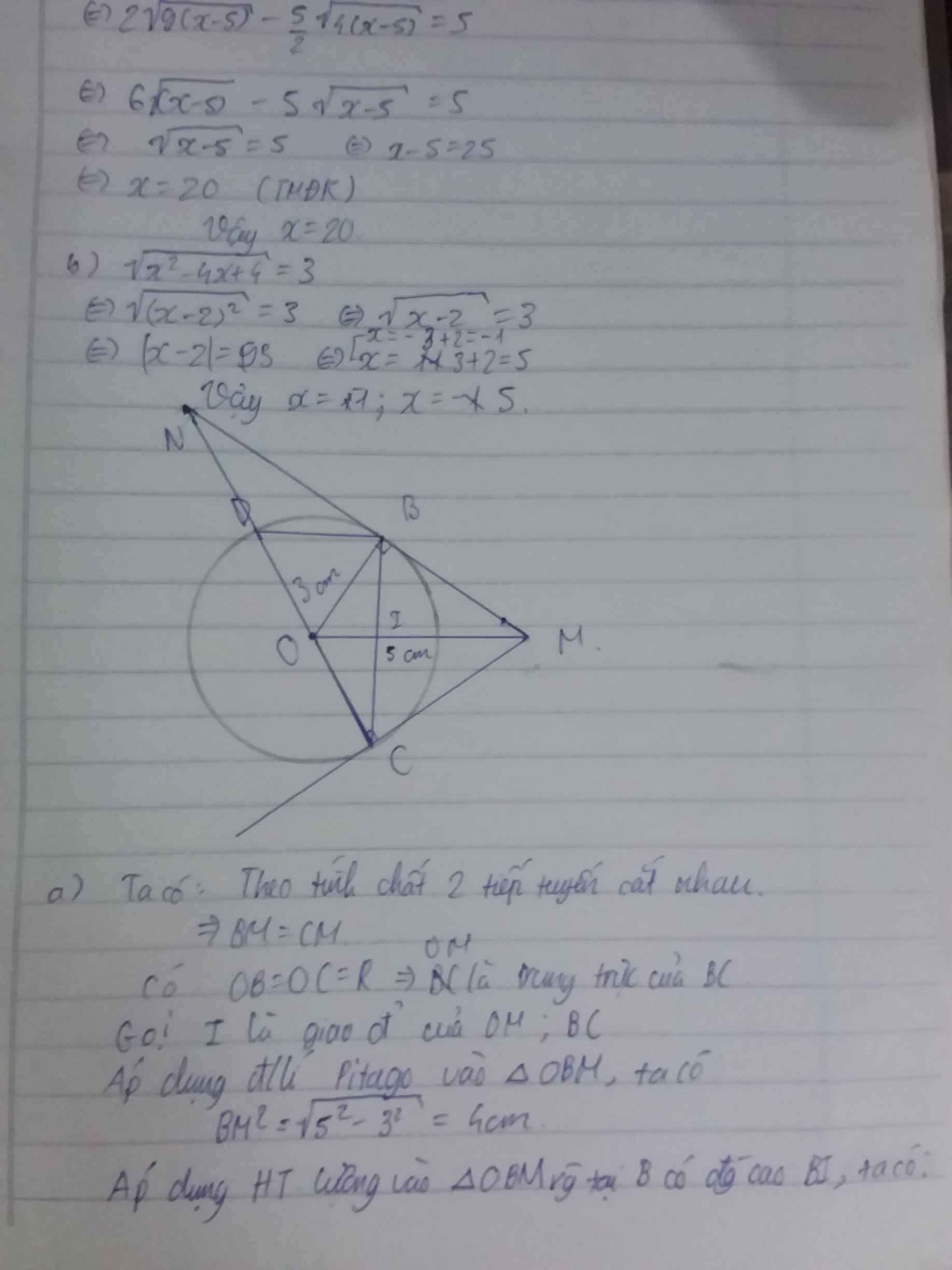
Xét ΔOMS vuông tại M có \(OS^2=MS^2+MO^2\)
=>\(MS^2+3^2=5^2\)
=>\(MS^2=5^2-3^2=16\)
=>\(MS=\sqrt{16}=4\left(cm\right)\)
Xét ΔOMS vuông tại M có MH là đường cao
nên \(MH\cdot OS=MO\cdot MS\)
=>\(MH\cdot5=3\cdot4=12\)
=>\(MH=\dfrac{12}{5}=2,4\left(cm\right)\)
H là trung điểm của MN
=>\(MN=2\cdot MH=4,8\left(cm\right)\)
Ta có: SM=SN
mà SM=4cm
nên SN=4cm
a: Xét (O) có
MN,MP là tiếp tuyến
nên MN=MP
mà ON=OP
nên OM là trung trực của NP
b: Gọi giao của NP và OM là H
=>H là trung điểm của NP và NP vuông góc với OM tại H
\(NM=\sqrt{4^2-2^2}=2\sqrt{3}\left(cm\right)\)
=>\(NH=2\cdot\dfrac{2\sqrt{3}}{4}=\sqrt{3}\left(cm\right)\)
=>\(NP=2\sqrt{3}\left(cm\right)\)