giúp mik vs ạa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải thích:
Để nâng cao chất lượng cuộc sống và phát triển kinh tế cho người dân ở vùng núi, có thể đề xuất các giải pháp sau:
1. Đầu tư vào hạ tầng: Xây dựng và cải thiện hệ thống giao thông, điện lực, nước sạch và viễn thông để kết nối vùng núi với các khu vực khác. Điều này sẽ tạo điều kiện thuận lợi cho việc vận chuyển hàng hóa, phát triển du lịch và thu hút đầu tư.
2. Phát triển nông nghiệp và chế biến sản phẩm: Hỗ trợ người dân vùng núi trong việc áp dụng các phương pháp nông nghiệp hiện đại, đa dạng hóa cây trồng và chăn nuôi. Đồng thời, xây dựng các cơ sở chế biến sản phẩm nông nghiệp để gia tăng giá trị gia tăng và tạo ra việc làm cho người dân địa phương.
3. Đào tạo và phát triển nguồn nhân lực: Đầu tư vào giáo dục và đào tạo để nâng cao trình độ chuyên môn và kỹ năng cho người dân vùng núi. Điều này sẽ giúp họ có cơ hội tìm kiếm việc làm tốt hơn và tham gia vào các ngành kinh tế mới.
4. Phát triển du lịch: Tận dụng tiềm năng du lịch của vùng núi bằng cách xây dựng các điểm đến du lịch hấp dẫn, khám phá và bảo tồn các di sản văn hóa, thiên nhiên đặc biệt của vùng núi. Điều này sẽ tạo ra nguồn thu nhập thêm cho người dân địa phương và thúc đẩy phát triển kinh tế.
Lời giải:
- Đầu tư vào hạ tầng
- Phát triển nông nghiệp và chế biến sản phẩm
- Đào tạo và phát triển nguồn nhân lực
- Phát triển du lịch

\(A=3+3^2+...+3^{2005}\)
\(\Rightarrow3A=3^2+3^3+...+3^{2006}\)
\(\Rightarrow3A-A=3^{2006}-3\)
\(\Rightarrow2A=3^{2006}-3\)
\(\Rightarrow2A+3=3^{2006}\) là 1 lũy thừa của 3 (đpcm)
4.
\(B=1+1+2+2^2+2^3+...+2^{100}\)
\(2B=2+2+2^2+...+2^{101}\)
\(\Rightarrow2B-B=2+2^{101}-\left(1+1\right)=2^{101}\)
\(\Rightarrow B=2^{101}\) là 1 lũy thừa của 2 (đpcm)

Bài 1:
\(A=2+2^2+2^3+...+2^{2003}+2^{2004}\)
\(=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{2002}+2^{2003}+2^{2004}\right)\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2002}\left(1+2+2^2\right)\)
\(=7\cdot\left(2+2^4+...+2^{2002}\right)⋮7\)
Bài 2:
\(A=2+2^2+2^3+2^4+...+2^{59}+2^{60}\)
\(=\left(2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8\right)+...+\left(2^{57}+2^{58}+2^{59}+2^{60}\right)\)
\(=2\left(1+2+2^2+2^3\right)+2^5\left(1+2+2^2+2^3\right)+...+2^{57}\left(1+2+2^2+2^3\right)\)
\(=15\cdot\left(2+2^5+...+2^{57}\right)⋮15\)
Bài 3:
\(A=1+3+3^2+3^3+...+3^{1990}+3^{1991}\)
\(=\left(1+3+3^2\right)+\left(3^3+3^4+3^5\right)+...+\left(3^{1989}+3^{1990}+3^{1991}\right)\)
\(=13+3^3\left(1+3+3^2\right)+...+3^{1989}\left(1+3+3^2\right)\)
\(=13\left(1+3^3+...+3^{1989}\right)⋮13\)
Bài 4:
\(A=4+4^2+4^3+4^4+...+4^{23}+4^{24}\)
\(=\left(4+4^2\right)+\left(4^3+4^4\right)+...+\left(4^{23}+4^{24}\right)\)
\(=\left(4+4^2\right)+4^2\left(4+4^2\right)+...+4^{22}\left(4+4^2\right)\)
\(=20\left(1+4^2+...+4^{22}\right)⋮20\)



Bài 33:
a: \(x^2-3x+2=\left(x-2\right)\left(x-1\right)\)




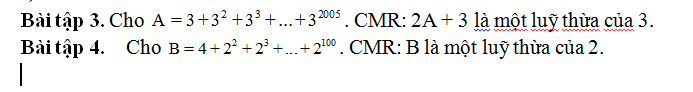

 giúp em vs ạa
giúp em vs ạa
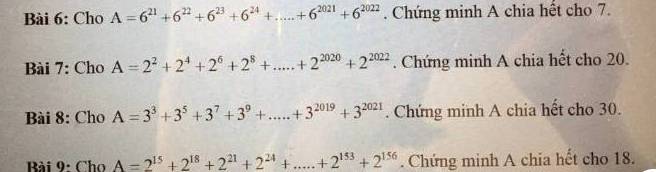


 Mik cần gấp lms luôn ạa mng giúp mik vớii
Mik cần gấp lms luôn ạa mng giúp mik vớii
