Giúp mình câu 37 với. Xin cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}A'B'\perp AA'\\A'B'\perp A'C'\end{matrix}\right.\) \(\Rightarrow A'B'\perp\left(ACC'A'\right)\)
\(\Rightarrow\widehat{B'CA'}\) là góc giữa \(B'C\) và (ACC'A') \(\Rightarrow sin\widehat{B'CA'}=\dfrac{A'B'}{B'C}=\dfrac{1}{2\sqrt{5}}\)
Mặt khác:
\(CC'||AA'\Rightarrow CC'||\left(ABB'A'\right)\Rightarrow d\left(A'B;CC'\right)=d\left(CC';\left(ABB'A'\right)\right)=d\left(C;\left(ABB'A'\right)\right)=AC\)
\(\Rightarrow AC=a\sqrt{3}\Rightarrow AB=AC.tan30^0=a\)
\(\Rightarrow B'C=2\sqrt{5}A'B'=2a\sqrt{5}\) ; \(BC=\dfrac{AB}{sin30^0}=2a\)
\(\Rightarrow BB'=\sqrt{B'C^2-BC^2}=4a\)
\(V=\dfrac{1}{2}AB.AC.BB'=2a^3\sqrt{3}\)

Từ S kẻ \(SH\perp AC\) (1)
Ta có: \(\left\{{}\begin{matrix}SB\perp SA\\SB\perp SC\end{matrix}\right.\) \(\Rightarrow SB\perp\left(SAC\right)\Rightarrow SB\perp AC\) (2)
(1);(2) \(\Rightarrow AC\perp\left(SBH\right)\)
Trong mp (SBH), từ S kẻ \(SK\perp BH\Rightarrow SK\perp\left(ABC\right)\)
\(\Rightarrow SK=d\left(S;\left(ABC\right)\right)\)
\(\dfrac{1}{SH^2}=\dfrac{1}{SA^2}+\dfrac{1}{SC^2}\Rightarrow SH=\dfrac{SA.AC}{\sqrt{SA^2+SC^2}}=\dfrac{a\sqrt{3}}{2}\)
\(\dfrac{1}{SK^2}=\dfrac{1}{SB^2}+\dfrac{1}{SH^2}\Rightarrow SK=\dfrac{SB.SH}{\sqrt{SB^2+SH^2}}=\dfrac{a\sqrt{66}}{11}\)

\(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\) (1)
Trong mp đáy, kẻ \(AH\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAH\right)\)
Trong mp (SAH), kẻ \(AK\perp SH\Rightarrow AK\perp\left(SBC\right)\)
Hệ thức lượng tam giác vuông ABC: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow AH=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Hệ thức lượng tam giác vuông SAH:
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}\Rightarrow AK=\dfrac{AH.SA}{\sqrt{AH^2+SA^2}}=\dfrac{2a\sqrt[]{57}}{19}\)

Cái chức năng xoay ảnh như bù nhìn vậy :v
Nguyên hoá \(\left(0,48;0,56;0,72\right)=\left(48;56;72\right)\Rightarrow BCNN\left(48;56;72\right)=1008\)
\(\Rightarrow\) 3 bậc trùng tại:\(\left\{{}\begin{matrix}\lambda_1:\dfrac{1008}{48}=21\Rightarrow so-van-sang-bac-1:k_1=21-1=20\\\lambda_2:\dfrac{1008}{56}=18\Rightarrow k_2=18-1=17\\\lambda_3=\dfrac{1008}{72}=14\Rightarrow k_3=14-1=13\end{matrix}\right.\)
\(\lambda_1\equiv\lambda_2:\dfrac{k_1}{k_2}=\dfrac{\lambda_2}{\lambda_1}=\dfrac{7}{6}=\dfrac{14}{12}=\dfrac{21}{18}\Rightarrow\) 2 vân bước sóng 1 trùng vơi bước sóng 2
\(\lambda_2\equiv\lambda_3:\dfrac{k_2}{k_3}=\dfrac{\lambda_3}{\lambda_2}=\dfrac{9}{7}=\dfrac{18}{14}\Rightarrow\) 1 vân bước sóng 2 trùng với bước sóng 3
\(\lambda_1\equiv\lambda_3:\dfrac{k_1}{k_3}=\dfrac{\lambda_3}{\lambda_1}=\dfrac{3}{2}=\dfrac{6}{4}=\dfrac{9}{6}=\dfrac{12}{8}=\dfrac{15}{10}=\dfrac{18}{12}=\dfrac{21}{14}\Rightarrow\) 6 vân bước sóng 1 trùng với bước sóng 3
\(\Rightarrow van-sang:k_1+k_2+k_3-6-1-2=41\left(van\right)\)

Không ai vẽ hình khi làm bài mặt cầu Oxyz đâu bạn, chỉ cần đại số hóa nó là được.
Gọi I là tâm mặt cầu, do mặt cầu tiếp xúc (Q) tại H nên \(IH\perp\left(Q\right)\)
\(\Rightarrow\) Đường thẳng IH nhận vtpt của (Q) là 1 vtcp
\(\Rightarrow\) IH nhận (1;1;-1) là 1 vtcp
Phương trình IH: \(\left\{{}\begin{matrix}x=1+t\\y=-1+t\\z=-t\end{matrix}\right.\)
I vừa thuộc IH vừa thuộc (P) nên là giao điểm của IH và (P)
\(\Rightarrow\) Tọa độ I thỏa mãn:
\(2\left(1+t\right)+\left(-1+t\right)+\left(-t\right)-3=0\)
\(\Rightarrow t=1\Rightarrow I\left(2;0;-1\right)\)
\(\Rightarrow\overrightarrow{IH}=\left(-1;-1;1\right)\Rightarrow R=IH=\sqrt{3}\)
Phương trình (S):
\(\left(x-2\right)^2+y^2+\left(z+1\right)^2=3\)

b: AD là phân giác
=>DB/AB=DC/AC
=>DB/DC=AB/AC=3/4
=>DB/3=DC/4
mà DB+DC=BC=14
nên DB/3=DC/4=14/7=2
=>DB=6cm; DC=8cm

Hàm bậc 2 có \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=6-m\end{matrix}\right.\) nên nghịch biến trên khoảng \(\left(-\infty;6-m\right)\)
Hàm nghịch biến trên khoảng đã cho khi:
\(6-m\ge2\Rightarrow m\le4\)
\(\Rightarrow\) Có 4 giá trị nguyên dương của m

\(\Leftrightarrow\left(4x-3\right)\left(4x+3-x\right)=0\)
=>(4x-3)(3x+3)=0
=>x=3/4 hoặc x=-1

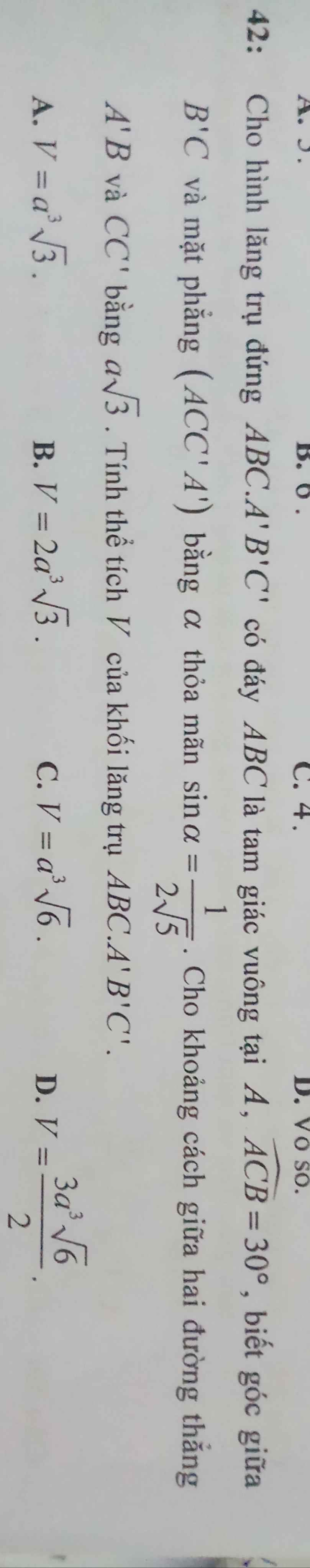
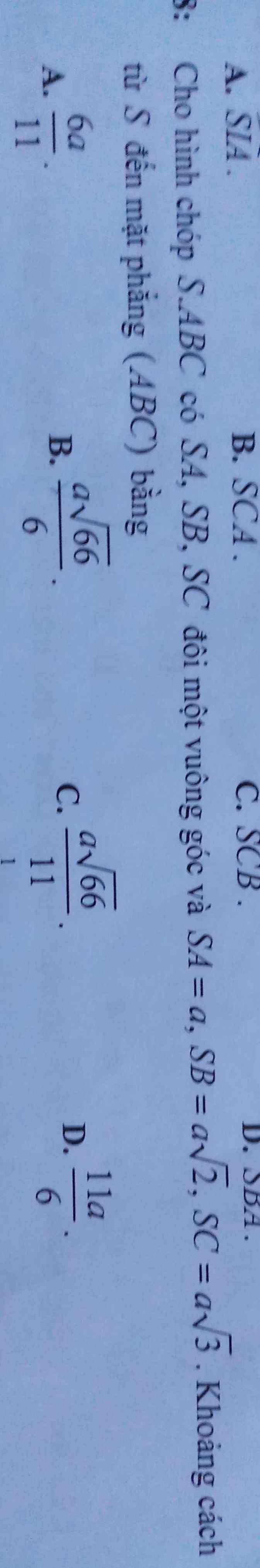



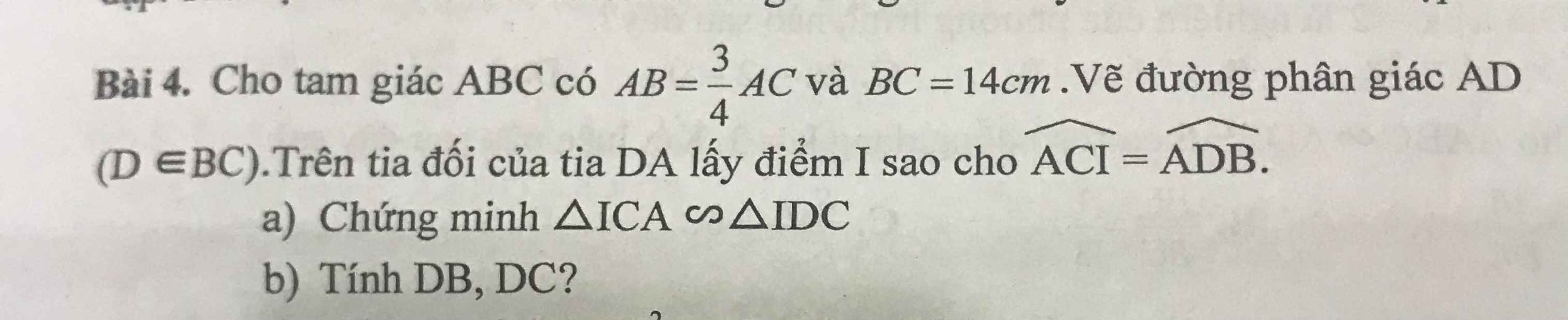
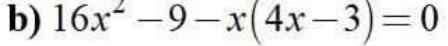
\(\omega=\sqrt{\dfrac{g}{l}}\Rightarrow l=\dfrac{g}{\omega^2}=\dfrac{9,8}{3,5^2}=0,8\left(m\right)=80\left(cm\right)\)
\(\Rightarrow s=4\cos\left(3,5t+\dfrac{\pi}{2}\right)\)
t=0 thì con lắc đang ở vị trí có pha là pi/2, nghĩa là ở VTCB, vậy đi được uãng đường 4cm nghĩa là đi từ VTCB đến biên âm
\(\Rightarrow t=\dfrac{T}{4}=\dfrac{2\pi}{\omega.4}=\dfrac{2.3,14}{3,5.4}=0,45\left(s\right)\)