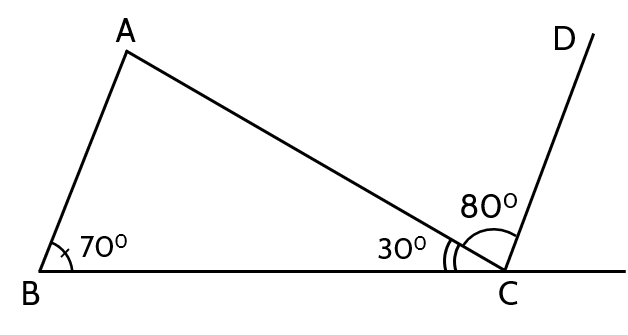
(0,75 điểm) Hãy chứng tỏ trong hình vẽ trên có$AB$ // $CD$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 9 2016
Có: \(\widehat{BCA}+\widehat{ACD}=30+80=110\)
\(\widehat{ABC}+\widehat{BCD}=70+110=180\)
=>AB//CD ( Cặp góc trong cùng phía bù nhau)
IM
25 tháng 9 2016
Xét \(\Delta ABC\) có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\) ( bđt \(\Delta\))
\(\Rightarrow\widehat{A}+70^0+30^0=180^0\)
\(\Rightarrow\widehat{A}=80^0\)
\(\Rightarrow\widehat{A}=\widehat{ACB}\)
Mà \(\widehat{A};\widehat{ABC}\) đồng vị
=> AB // CD
25 tháng 9 2016
Ta có hình vẽ:
Kẻ tia Am là tia đối của AB
Ta có: BAE + EAm = 180o (kề bù)
=> 100o + EAm = 180o
=> EAm = 180o - 100o
=> EAm = 80o
Lại có: EAm + mAC = EAC
=> 80o + mAC = 120o
=> mAC = 120o - 80o
=> mAC = 40o
Vì mAC + ACD = 40o + 140o = 180o mà mAC và ACD là 2 góc trong cùng phía
=> Am // CD
Mà AB là tia đối của Am => AB // CD (đpcm)
CM
21 tháng 12 2019
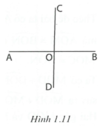
a) Ba đường thẳng cắt nhau tại O tạo thành 6 tia. Số góc do 6 tia tạo ra là: 6.5 2 = 15 (góc).
b) Xét hai đường thẳng AB và CD trong ba đường thẳng đã cho (h.1.11). Hai đường thẳng này tạo thành bốn góc không có điểm trong chung. Tổng của bốn góc này bằng 360 ° nên trong bốn góc đó phải tồn tại một góc lớn hơn hoặc bằng 90 ° .
Thật vậy, nếu mỗi góc đó đều nhỏ hơn 90 ° thì tổng của chúng nhỏ hơn 90 ° .4 = 360 ° : vô lí.
Giả sử góc tồn tại nói trên là góc BOD.
- Nếu B O D ^ > 90 ° thì A O C ^ = B O D ^ > 90 ° , bài toán đã giải xong.
- Nếu B O D ^ = 90 ° thì ta xét tiếp đường thẳng thứ ba MN đi qua O (h.1.12).
Giả sử tia ON nằm trong góc BOD. Khi đó góc BON là góc nhọn do đó A O N ^ là góc tù (vì B O N ^ và A O N ^ là hai góc kề bù). Góc AON là góc tù thì góc BOM là góc tù (vì B O M ^ = A O N ^ ).
Vậy luôn tồn tại hai góc tù trong số 15 góc được tạo thành.
Chứng tỏ hai tia đối nhau
16 tháng 10 2021
Gọi Ax đối AB
\(\Rightarrow\widehat{xAE}=180^0-\widehat{BAE}=80^0\left(kề.bù\right)\\ \Rightarrow\widehat{xAC}=\widehat{EAC}-\widehat{xAE}=120^0-80^0=40^0\\ \Rightarrow\widehat{xAC}+\widehat{ACD}=40^0+140^0=180^0\)
Mà 2 góc này ở vị trí trong cùng phía nên Ax//CD
Mà Ax đối AB nên AB//CD
VT
1 tháng 9 2019
** Muốn dựng ảnh của một vật AB qua thấu kính phân kì khi AB vuông góc với trục chính, A nằm trên trục chính, ta làm như sau:
Dùng hai trong ba tia sáng đã học để dựng ảnh B’ của điểm B.
+ Tia BI đi song song với trục chính nên cho tia ló có đường kéo dài đi qua F
+ Tia tới BO là tia đi quang tâm O nên cho tia ló đi thẳng
+ Hai tia ló trên có đường kéo dài giao nhau tại B’, ta thu được ảnh ảo B’ của B qua thấu kính.
+ Từ B’ hạ vuông góc với trục của thấu kính, cắt trục chính tại điểm A’. A’ là ảnh của điểm A. A’B’ là ảnh ảo của AB tạo bởi thấu kính phân kỳ. (Hình 45.2a)
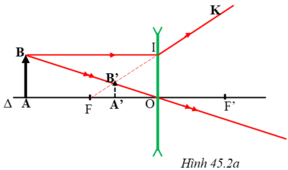
** Ta dựa vào tia đi song song trục chính và tia đi qua quang tâm để dựng ảnh A'B' của AB. Khi tịnh tiến AB luôn vuông góc với trục chính thì tại mọi vị trí, tia BI luôn không đổi, cho tia ló IK cũng không đổi. Do đó tia BO luôn cắt tia IK kéo dài tại B' nằm trong đoạn FI → Hình chiếu A’ của B’ lên trục chính nằm trong đoạn OF. Chính vì vậy, ảnh A'B' luôn nằm trong khoảng tiêu cự của thấu kính.
1 tháng 2 2022
b: Trên tia Ox, ta có: OA<OB(1cm<5cm)
nên điểm A nằm giữa hai điểm O và B
=>OA+AB=OB
=>AB=4cm
Trên đoạn AB, ta có: AC<AB
nên điểm C nằm giữa hai điểm A và B
c: Ta có: C nằm giữa A và B
mà AC=1/2AB
nên C là trung điểm của AB
d: B là trung điểm của CD
nên BC=BD=2cm
=>OB+BD=OD
=>OD=5+2=7(cm)
Xét tg ABC có
\(\widehat{BAC}=180^o-\widehat{ABC}-\widehat{ACB}\) (tổng các góc trong của 1 tg \(=180^o\) )
\(\Rightarrow\widehat{BAC}=180^o-70^o-30^o=80^o=\widehat{ACD}\)
Hai góc \(\widehat{BAC}=\widehat{ACD}\) ở vị trí so le trong => AB//CD