tìm a , b biết
10,1 x ab = 7a,b5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TG
23 tháng 11 2016
a,b x 10,1 = 3b,a5
Mà a,b x 10,1 = ab,ab
Nên a = 3 ; b = 5
Và a,b = 3,5
NH
0
NT
0
CT
1
5 tháng 11 2016
Do \(ab+1>3\)
Nên \(ab+1\) là số lẻ
Suy ra: \(a\) là số chẵn hoặc \(b\) là số chẵn
Suy ra \(a=2\) hoặc \(b=2\)
+) Khi \(a=2\)
Nếu \(b\) chia \(3\) dư \(1\) thì \(7a+b=14+b\) chia hết cho \(3\) (Loại) Nếu \(b\) chia \(3\) dư \(2\) thì \(ab+1=2b+1\) chia hết cho \(3\) (Loại) Vậy \(b\)chia hết cho \(3\)Suy ra: \(b=3\)
+) Khi \(b=2\)
Cũng xét tương tự bạn nhé!
Các cặp số là \(\left(3;2\right)\) và
5 tháng 11 2016
chỗ khi a = 2, nếu b chia 3 dư 2 => ab + 1 = 2b + 1 = 2.(3k + 2) + 1
= 6k + 4 + 1 = 6k + 5 chia hết cho 3 sai r`
a=2;b=5 thử lại vx đúng
22 tháng 7 2016
a) 4,25 + x = 10,1
x = 10,1 - 4,25
x = 5,85
b) x - 24,25 = 2,4
x = 2,4 + 24,25
x = 26,65
DN
1
AH
Akai Haruma
Giáo viên
12 tháng 10
Lời giải:
$ab+11$ là số nguyên tố, mà $ab+11>2$ nên $ab+11$ là số nguyên tố lẻ.
$\Rightarrow ab$ chẵn.
$\Rightarrow$ trong 2 số sẽ có ít nhất 1 số chẵn.
TH1: $a$ chẵn. Do $a$ nguyên tố nên $a=2$
Khi đó cần tìm $b$ sao cho $b, 14+b$ và $2b+11$ nguyên tố
Nếu $b\vdots 3$ thì $b=3$ (do $b$ nguyên tố). Khi đó $14+b=17, 2b+11=17$ là snt (hoàn toàn thỏa mãn)
Nếu $b$ chia 3 dư 1 thì $14+b\vdots 3$. Mà $14+b>3$ nên không là snt (loại)
Nếu $b$ chia 3 dư 2 thì $2b+11\vdots 3$. Mà $2b+11>3$ nên không là snt (loại)
TH2: $b$ chẵn. Do $b$ nguyên tố nên $b=2$
Khi đó cần tìm a sao cho $a, 7a+2, 2a+11$ là snt.
Nếu $a\vdots 3$ thì $a=3$. Khi đó: $7a+2=23, 2a+11=17$ là snt (tm)
Nếu $a$ chia 3 dư 1 thì $7a+2\vdots 3$. Mà $7a+2>3$ nên không là snt (loại)
Nếu $a$ chia $3$ dư 2 thì $2a+11\vdots 3$. Mà $2a+11>3$ nên không là snt (loại)
Vậy phân số cần tìm là $\frac{2}{3}$ hoặc $\frac{3}{2}$
PT
1
CM
7 tháng 6 2017
Ta có: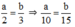 
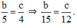
Suy ra: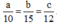 
Theo tính chất dãy tỉ số bằng nhau ta có: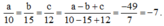 
Ta có:
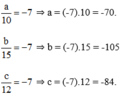
Vậy a = -70; b = -105; c = -84.
TH
0
HN
0
2 tháng 8 2020
\(\left(a\right)\overline{a3}-17=66\)
\(\overline{a3}=66+17=83\)
a = 8
\(\left(b\right)\overline{a42}+\overline{b5}+\overline{10c}=789\)
\(a\cdot100+40+2+b\cdot10+5+100+c=789\)
\(\overline{abc}+147=789\)
\(\overline{abc}=789-147=642\)
a = 6; b = 4; c = 2
\(\left(c\right)\overline{ab}+281=\overline{ab0}+2\)
\(281-2=\overline{ab0}-\overline{ab}\)
\(279=\overline{ab}\cdot9\)
\(\overline{ab}=\frac{279}{9}=31\)
a = 3; b = 1
\(\left(d\right)\overline{2ab2}=\overline{ab}\cdot11+1989\)
\(2002+\overline{ab0}=\overline{ab}\cdot11+1989\)
\(2002-1989=\overline{ab}\cdot11-\overline{ab0}\)
\(\overline{ab}=13\)
a = 1; b = 3
\(\left(e\right)\overline{ab}\cdot6=\overline{a0b}\)
\(\left(a\cdot10+b\right)\cdot6=a\cdot100+b\)
\(a\cdot60+b\cdot6=a\cdot100+b\)
\(b\cdot6-b=a\cdot100-a\cdot60\)
\(b\cdot5=a\cdot40\)
\(b=a\cdot8\)
Suy ra a = 1; b = 8
a=7
b=5