Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Do EC// AB nên \(\widehat{ECD}=\widehat{ABC}=60^o\)
Do ED// AC nên \(\widehat{EDC}=\widehat{ACB}=60^o\)
Xét tam giác ECD có \(\widehat{ECD}=\widehat{EDC}=60^o\Rightarrow\widehat{CED}=60^o\)
Suy ra ECD là tam giác đều.
b) Ta có :
\(\widehat{BCE}=\widehat{BCA}+\widehat{ACE}=60^o+\widehat{ACE}=\widehat{ECD}+\widehat{ACE}=\widehat{ACD}\)
Xét tam giác BCE và tam giác ACD có:
BC = AC (gt)
CD = CE (Do tam giác ECD đều)
\(\widehat{BCE}=\widehat{ACD}\) (cmt)
\(\Rightarrow\Delta BCE=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow BE=AC\)
c) Do \(\Delta BCE=\Delta ACD\Rightarrow\widehat{CBI}=\widehat{CAI}\)
Vậy thì \(\widehat{CBJ}+\widehat{BJC}=\widehat{JAI}+\widehat{JAI}\)
\(\Rightarrow180^o-\left(\widehat{CBJ}+\widehat{BJC}\right)=180^o-\left(\widehat{JAI}+\widehat{JAI}\right)\)
\(\Rightarrow\widehat{AIJ}=\widehat{JCB}=60^o\)
\(\Rightarrow\widehat{BID}=180^o-60^o=120^o\) (Hai góc kề bù)
\(\Rightarrow\widehat{BID}=2\widehat{BAC}\)
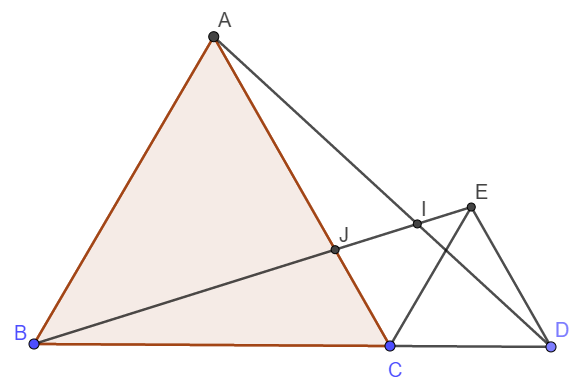
a)+Có AB//Cx(gt)=> góc ABC= góc ECD(2 góc đồng vị )
Mà góc ABC =60 (vì tam giác ABC đều)=>góc ECD= ABC=60
+Có AC//Dy(gt)=> góc ACB= góc EDC (2 góc đồng vị)
Mà góc ACB =60 (vì tam giác ABC đều)=>góc EDC= ACB=60
+Có ECD=60; EDC=60=>ECD=EDC=60
=>tam giác ECD đều (dhnb tam giác đều)
b) +Có góc ACB+ACD=180(kề bù)
+Có góc ECD+ECB=180(kề bù)
Mà góc ACB=ECD=60
=>Góc ACD = góc ECB
Xét tam giác ACD và tam giác BCE
+Có CD=ED(tam giác ECD đều)
góc ACD=góc ECB(cmt)
AC=BC((tam giác ABC đều)
=>tam giác ACD =BCE