Cho 4 điểm A,B,C,D bất kì .Hãy xác định số đường thẳng vẽ đc từ 4 điểm trên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) ________________________
b)_____A____________B___________________C___________________D__________________
c)_____A____________B___________________C___________________D__________________ .E
d)ABC ; BCD; ACD ;
dường thẳng AB ( AC;AD;BC;BD;CD)

Gọi I là trung điểm của OA.
Có AB,AC là tiếp tuyến của (O;R)
=> OB⊥AB; OC⊥CA
Xét △ABO vuông tại B có BI là đường trung tuyến
=> BI = IO =IA (1)
Xét △ACO vuông tại C có CI là đường trung tuyến
=> CI =IO =IA (2)
Từ (1) và (2) => IB = IC=IA = IO
=> A,B,O,C cùng nằm trên một đường tròn.

a) Với 4 điểm A, B, C, D cho trước trong đó không có ba điểm bất kì nào thẳng hàng thì có thể vẽ được 6 đường thẳng là: AB , AC , AD , BC , BD , CD .
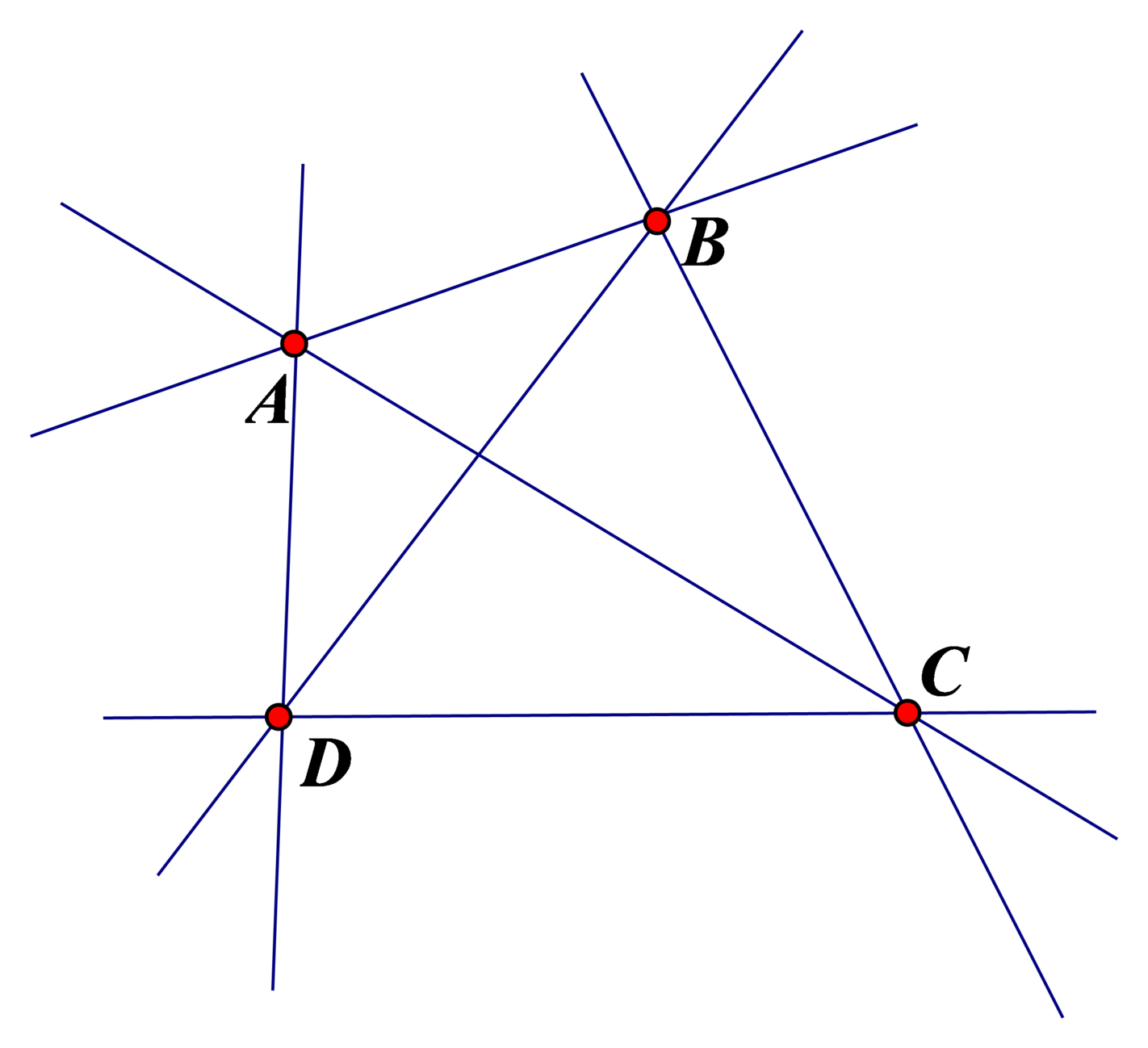
b) Với 5 điểm A, B, C, D, E cho trước trong đó không có ba điểm bất kì nào thẳng hàng thì có thể vẽ được 10 đường thẳng là: AB , AC , AD , AE , BC , BD , BE , CD , CE , DE .
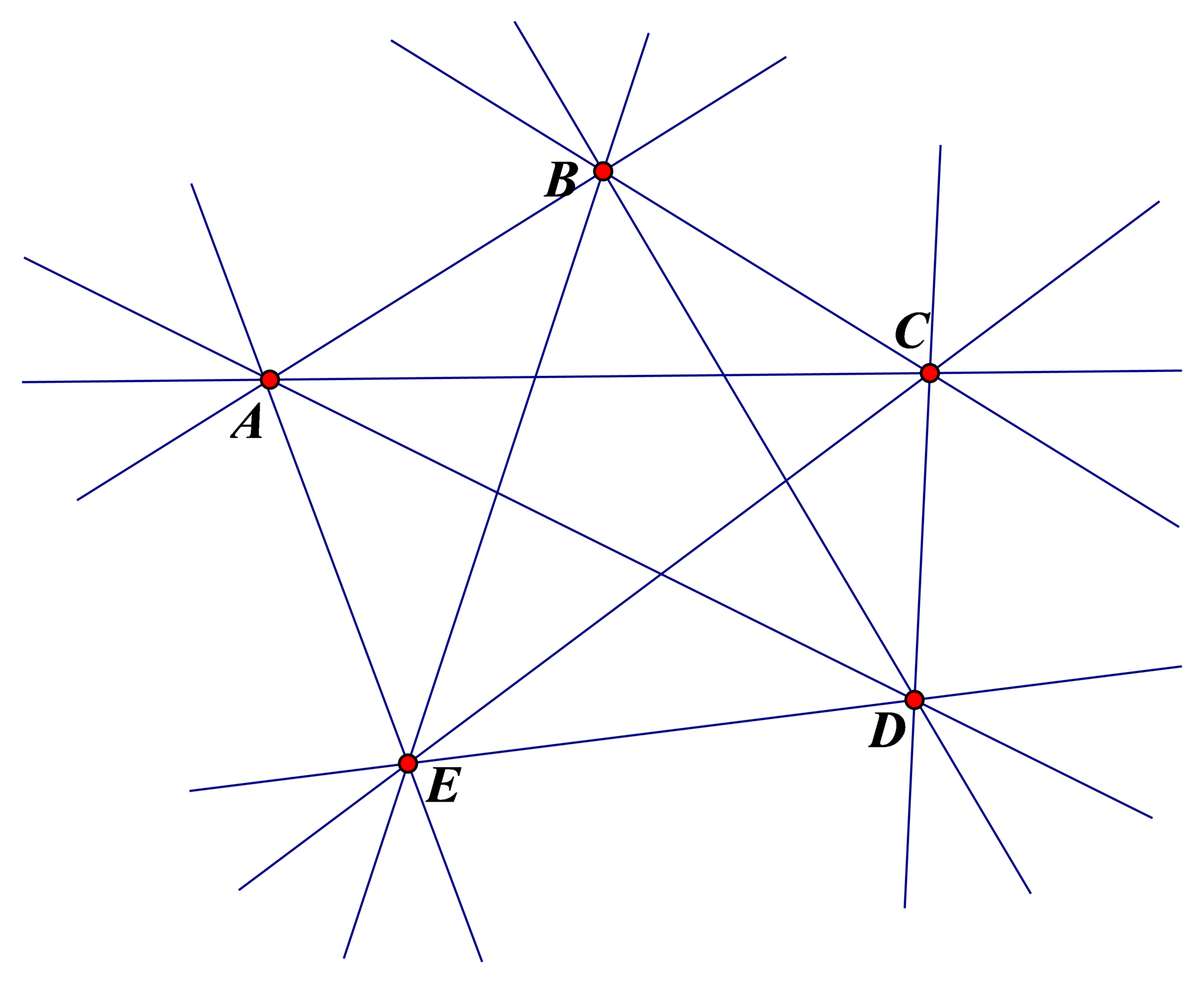
c) Chọn một trong số n điểm đã cho rồi nối điểm đó với n-1 điểm còn lại ta được n-1 đường thẳng.
Làm như vậy với tất cả n điểm ta được n(n-1) đường thẳng. Nhưng mỗi đường thẳng được tính hai lần, do đó ta vẽ được n . n − 1 2 đường thẳng.

