Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

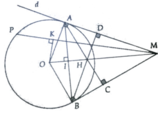
a, HS tự làm
b, Chú ý O K M ^ = 90 0 và kết hợp ý a) => A,M,B,O,K ∈ đường tròn đường kính OM
c, Sử dụng hệ thức lượng trong tam giác vuông OAM ( hoặc có thể chứng minh tam giác đồng dạng)
d, Chứng minh OAHB là hình bình hành và chú ý A,B thuộc (O;R) suy ra OAHB là hình thoi
e, Chứng minh OH ⊥ AB, OMAB => O,H,M thẳng hàng

a) Nối O với N. Ta có \(\widehat{OAN}\)=\(\widehat{OBN}\)=\(\widehat{ONM}\)=90° →các góc này nội tiếp chắn nửa đường tròn đường kính ON →O,A,B,N,M cùng nằm trên đường tròn đường kính ON.
b) Nối A với M. Xét tứ giác nội tiếp OANB(chứng minhnội tiếp trước)ta có \(\widehat{AMO}\)=\(\frac{1}{2}\)\(\widebat{OA}\);\(\widehat{OAB}\)=\(\frac{1}{2}\)\(\widebat{OB}\) mà
- \(\widebat{OA}\)=\(\widebat{OB}\)→\(\widehat{AMO}\)=.\(\widehat{OAB}\)=\(\widehat{OAI}\)Xét tam giác OAI và tam giác OMA: \(\widehat{O}\)chung ,\(\widehat{OAI}\)=\(\widehat{AMO}\)\(\Rightarrow\)hai tam giác đồng dạng (g.g) \(\Rightarrow\)\(\frac{OI}{OA}\)=\(\frac{OA}{OM}\)\(\Leftrightarrow\)OI.OM=\(^{OA^2}\)=Rbình.
- c)

a, Gọi AM giao CH tại K
BM giao HD tại T
AC , AH là tt (M) => góc MKH = 90 độ
TT góc KMT = 90 độ
góc AMB = 90 độ
=> góc KHT = 90 độ => Tam giác CHD vuông tại H
Ta có MC = MD = MH ( =R )
=> M thuộc DC => đpcm
Tam giác OMA cân tại O => OMA = OAM
CMA + CAM = 90 độ
CAM = MAH> OAM + CMA = 90 độ => OMA + AMC = 90 độ => OM vuông góc DC => đpcm
c, Tam giác OMI vuông tại M ( MI là tt ) => MO^2= HO.OI =R^2
=> đpcm
Gọi I là trung điểm của OA.
Có AB,AC là tiếp tuyến của (O;R)
=> OB⊥AB; OC⊥CA
Xét △ABO vuông tại B có BI là đường trung tuyến
=> BI = IO =IA (1)
Xét △ACO vuông tại C có CI là đường trung tuyến
=> CI =IO =IA (2)
Từ (1) và (2) => IB = IC=IA = IO
=> A,B,O,C cùng nằm trên một đường tròn.