2xy+7=3(x-y)+1
Tìm x,y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

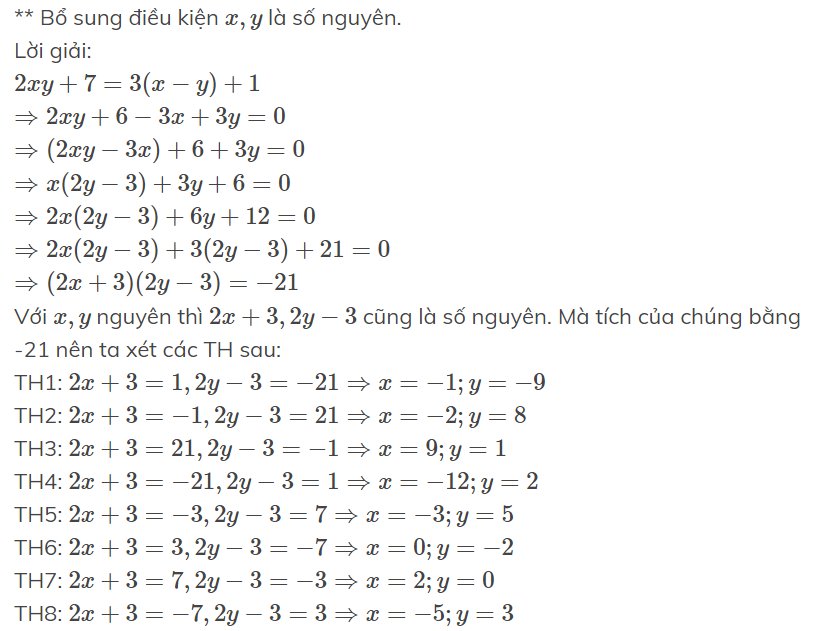

\(D\le\dfrac{1}{2}\left(1+\dfrac{x}{1+yz}\right)+\dfrac{1}{2}\left(1+\dfrac{y}{1+zx}\right)+\dfrac{z}{2+2xy}\)
\(=1+\dfrac{x}{2\left(1+yz\right)}+\dfrac{y}{2\left(1+zx\right)}+\dfrac{z}{2\left(1+xy\right)}\)
Do \(0\le x;y;z\le1\)
\(\Rightarrow\left(1-x\right)\left(1-y\right)\ge0\Leftrightarrow xy+1\ge x+y\)
\(\Leftrightarrow2\left(xy+1\right)\ge xy+1+x+y\ge x+y+z\)
\(\Rightarrow\dfrac{z}{2\left(1+xy\right)}\le\dfrac{z}{x+y+z}\)
Tương tự: \(\dfrac{x}{2\left(1+yz\right)}\le\dfrac{x}{x+y+z}\) ; \(\dfrac{y}{2\left(1+zx\right)}\le\dfrac{y}{x+y+z}\)
Cộng vế:
\(P\le1+\dfrac{x}{x+y+z}+\dfrac{y}{x+y+z}+\dfrac{z}{x+y+z}=2\)
Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(1;1;0\right)\)


Ta có x - y = 1 => x = y + 1
\(\dfrac{x+2}{9}=\dfrac{1}{y+2}\Rightarrow\left(x+2\right)\left(y+2\right)=9\)
\(\Leftrightarrow\left(3+y\right)\left(y+2\right)=9\Leftrightarrow y^2+5y-3=0\Leftrightarrow y=\dfrac{-5\pm\sqrt{37}}{2}\)
thay vào tìm x
ps nhưng số xấu quá bạn ạ, kiểm tra lại đề nhé
Ta có:
\(x-y=1\Rightarrow x=1+y\)
Thay vào
\(\dfrac{x-1}{9}+\dfrac{1}{3}=\dfrac{1}{y}+2\) \(\left(đk:y\ne0\right)\)
\(\dfrac{x+2}{9}=\dfrac{2y+1}{y}\)
\(\Leftrightarrow\dfrac{y+3}{9}=\dfrac{2y+1}{y}\)
\(\Leftrightarrow y^2+3y=18y+9\)
\(\Leftrightarrow y^2-15y-9=0\)
\(\Leftrightarrow\)\(\left(y-\dfrac{15}{2}\right)^2=\dfrac{261}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}y-\dfrac{15}{2}=\dfrac{\sqrt{261}}{2}\\y-\dfrac{15}{2}=-\dfrac{\sqrt{261}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{\sqrt{261}+15}{2}\\y=\dfrac{15-\sqrt{261}}{2}\end{matrix}\right.\)

\(x+y=1\Rightarrow y=1-x\)
\(P=x^3+\left(1-x\right)^3+x\left(1-x\right)\)
\(P=2x^2-2x+1=\dfrac{1}{2}\left(2x-1\right)^2+\dfrac{1}{2}\ge\dfrac{1}{2}\)
\(P_{min}=\dfrac{1}{2}\) khi \(x=y=\dfrac{1}{2}\)



Bài 1:
a) \(A=-\left(2x-5\right)^2+6\left|2x-5\right|+4=-\left[\left(2x-5\right)^2-6\left|2x-5\right|+9\right]+13=-\left(\left|2x-5\right|-3\right)^2+13\le13\)
\(maxA=13\Leftrightarrow\) \(\left[{}\begin{matrix}2x-5=3\\2x-5=-3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=1\end{matrix}\right.\)
b) \(B=-x^2-y^2+2x-6y+9=-\left(x^2-2x+1\right)-\left(y^2+6y+9\right)+19=-\left(x-1\right)^2-\left(y+3\right)^2+19\le19\)
\(maxC=19\Leftrightarrow\) \(\left\{{}\begin{matrix}x=1\\y=-3\end{matrix}\right.\)
Bài 2:
\(A=2\left(x^3-y^3\right)-3\left(x+y\right)^2=2\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x^2+2xy+y^2\right)=4\left(x^2+xy+y^2\right)-3\left(x^2+2xy+y^2\right)=x^2-2xy+y^2=\left(x-y\right)^2=2^2=4\)
bài 2
\(A=2\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x^2+2xy+y^2\right)\)
\(A=2.2\left(x^2+xy+y^2\right)-3\left(x^2+2xy+y^2\right)\)
\(A=\left(4x^2+4xy+4y^2\right)+\left(-3x^2-6xy-3y^2\right)\)
\(A=x^2-2xy+y^2=\left(x-y\right)^2=2^2=4\)

A=x^3 + y^3 + 3xy(x+y)
=x+3x^y+3xy^2+y^3
=(x+y)^3=2^3=8
B=x^2+2xy+y^2+4
=(x+y)^2+4=4+4=8
C=x^3+y^3+3xy(x+y)+7(x+y)
=(x+y)^3+7(x+y)
=2^3+7.2
=8+14=22

