Tìm 2 số biết :
a) Tổng của chúng bằng 2 và tích của chúng bằng 3/4
b) Tổng của chúng bằng 7 và tích của chúng bằng 14/3
c) Hiệu của chúng bằng 6 và tích của chúng bằng 13/4
d) Tích của chúng bằng 12 và các bình phương của chúng bằng 25
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hãy tích cho tui đi
Nếu bạn tích tui
Tui không tích lại đâu
THANKS

Coi hiệu của chúng là 1 phần thì tổng là 5 phần .
Số lớn là : ( 5 + 1 ) : 2 = 3 ( phần )
Số bé là : 3 - 1 = 2 ( phần )
Tích của 2 số là : 2 x 3 = 6 ( phần )
Mà tích của chúng là 192 nên giá trị 1 phần là : 192 : 6 = 32
Số bé là : 32 x 2 = 64
Số lớn là : 32 x 3 = 96


Bài 1: Tổng trừ hiệu chính bằng hai lần số bé, từ đề bài ta suy ra 2 lần hiệu bằng hai lần số bé. Nói cách khác hiệu bằng số bé hay số lớn gấp đối số bé.
Tích của số bé và số lớn chính là tích số bé và hai lần số bé chia 2 hay chính bằng số bé nhân số bé. Tổng bằng 3 lần số bé và bằng số bé nhân số bé nên số bé bằng 3 và số lớn bằng 6.
Bài 2: Tương tự. Ta tìm được số bé là 10, số lớn là 15.

Hai số phức có tổng bằng 3, tích bằng 4 là nghiệm của phương trình:
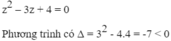
⇒ Phương trình có hai nghiệm: 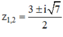
Vậy hai số cần tìm là 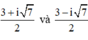
Lời giải:
a. Gọi 2 số cần tìm là $a$ và $b$
Theo bài ra:
$a+b=2\Rightarrow b=2-a$
$ab=\frac{3}{4}$
Thay $b=2-a$ thì:
$a(2-a)=\frac{3}{4}$
$\Leftrightarrow a^2-2a+\frac{3}{4}=0$
$\Leftrightarrow (a-\frac{3}{2})(a-\frac{1}{2})=0$
$\Leftrightarrow a=\frac{3}{2}$ hoặc $a=\frac{1}{2}$
Nếu $a=\frac{3}{2}$ thì $b=2-a=\frac{1}{2}$
Nếu $a=\frac{1}{2}$ thì $b=2-a=\frac{3}{2}$
b,c: Tương tự
d.
Gọi hai số cần tìm là $a$ và $b$
Theo bài ra ta có:
$ab=12$
$a^2+b^2=25$
$\Leftrightarrow (a+b)^2-2ab=25$
$\Leftrightarrow (a+b)^2=25+2ab=25+2.12=49$
$\Leftrightarrow a+b=\pm 7$
Đến đây lại đưa về dạng tìm 2 số biết tổng và tích giống như phần a.