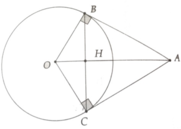
cho A ngoài (O). kẻ tiếp tuyến AB,AC. gọi H là giao của AO và BC
a. cmr AO\(⊥\)BC từ đó suy ra BH2=AH.HO
b.BD là đường kính của (O). tứ giác OACD là hình gì vì sao?
c. lấy N trên OB sao cho BN=2NO. trung trực của NC cắt OA tại M. cmr OA=3OM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 2 2023
a: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC và H là trung điểm của BC
b: Xét (O) co
ΔBDC nội tiếp
BD là đường kính
=>ΔBCD vuông tại C
=>DC//OA
CM
3 tháng 11 2017
a, HS tự làm
b,i, Áp dụng định lý Pytago tính được BH = 3 cm
Áp dụng hệ thức lược về cạnh góc vuông và đường cao trong tam giác vuông, tính được:
AB = AC = 2 3 cm => P A B C = 6 3 cm, S A B C = 3 3 c m 2
ii, Ta có: S A B O C = S A B C + S B O C = 4 3 c m 2
(Kĩ năng hình học của mình đã lên vài "cấp" sau khi ra câu c)
Câu c đề đúng phải là \(AO=3AM\), chứng minh như sau:
Nhận thấy \(OA\) là trung trực \(BC\) vậy \(M\) là giao của trung trực \(NC\) va trung trực \(BC\).
Tức là \(M\) là tâm đường tròn ngoại tiếp tam giác \(BNC\) và còn thêm \(M\) nằm trên trung trực \(BN\).
Gọi \(T\) là trung điểm \(BN\) thì \(BO=2BT\).
Theo định lí Thales cho tam giác \(OBA\) có \(MT\) song song với \(AB\):
\(AO=3AM\)(đpcm - ngắn gọn nhưng không dễ nhìn)