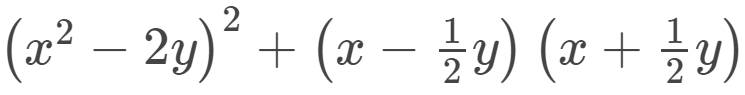
mọi người rút gọn biểu thức giúp mik vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
rút gọn biểu thức
7 tháng 2 2022
\(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x-1}-\dfrac{1}{\sqrt{x}+1}\left(đk:x\ne1,x\ge0\right)\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-2\sqrt{x}-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+\sqrt{x}-2\sqrt{x}-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
AM
7 tháng 2 2022
ĐKXĐ: \(x\ne1,x\ge0\)
\(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x-1}-\dfrac{1}{\sqrt{x}+1}=\)\(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x-1}-\dfrac{2\sqrt{x}}{x-1}-\dfrac{\sqrt{x}-1}{x-1}=\)\(\dfrac{x+\sqrt{x}-2\sqrt{x}-\sqrt{x}+1}{x-1}=\)\(\dfrac{x-2\sqrt{x}+1}{x-1}=\)\(\dfrac{(\sqrt{x}-1)^2}{x-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
6 tháng 11 2021
a: \(=25x^4-10x^3+5x^2\)
c: \(=2x^3-3x-5x^3-x^2+x^2=-3x^3-3x\)
12 tháng 11 2017
a)(x-3)(x+3)-(x+5)2+(x+1)(x+2)
=x2-9-x-10x-25+x2+2x+x+2
=2x2-8x-32
b)2 . 25 - 8 . 5 - 32=78
LS
1
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 4 2021
\(=\dfrac{1}{2}sin6x-\dfrac{1}{2}sin2x-\left(\dfrac{1}{2}sin4x-\dfrac{1}{2}sin2x\right)\)
\(=\dfrac{1}{2}sin6x-\dfrac{1}{2}sin4x\)
\(=cos5x.sinx\)
MP
2
5 tháng 10 2021
\(M=2x\left(-3x+2x^3\right)-x^2\left(3x^2-2\right)-x^2\left(x^2-4\right)\)
\(=-6x^2+4x^4-3x^4+2x^2-x^4+4x^2\)
\(=0\)
giúp mik với ạ chỉ cần rút gọn 6 cái biểu thức thui ạ .mong mn giúp đỡ.
AH
Akai Haruma
Giáo viên
26 tháng 8 2023
13.
$(x+4)^2+(x+5)(x-5)-2x(x+1)$
$=(x^2+8x+16)+(x^2-25)-(2x^2+2x)$
$=x^2+8x+16+x^2-25-2x^2-2x$
$=(x^2+x^2-2x^2)+(8x-2x)+(16-25)=6x-9$
14.
$(x-1)^2-2(x+3)(x-3)+4x(x-4)$
$=(x^2-2x+1)-2(x^2-9)+(4x^2-16x)$
$=x^2-2x+1-2x^2+18+4x^2-16x$
$=(x^2-2x^2+4x^2)+(-2x-16x)+(1+18)=3x^2-18x+19$
15.
$(y-3)(y+3)(y^2+9)-(y^2+2)(y^2-2)$
$=(y^2-9)(y^2+9)-(y^4-4)$
$=(y^4-81)-(y^4-4)=-81+4=-77$
16 tháng 12 2022
\(Q=\dfrac{x+y}{2\left(x-y\right)}-\dfrac{x-y}{2\left(x+y\right)}+\dfrac{x^2+y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x^2+2xy+y^2-x^2+2xy-y^2+2x^2+2y^2}{2\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{2x^2+2y^2+4xy}{2\left(x-y\right)\left(x+y\right)}=\dfrac{2\left(x+y\right)^2}{2\left(x-y\right)\left(x+y\right)}=\dfrac{x+y}{x-y}\)
AH
Akai Haruma
Giáo viên
21 tháng 5 2021
Lời giải:
\(A=\frac{2a^2+4}{(1-a)(1+a)}-\frac{1-\sqrt{a}+1+\sqrt{a}}{(1+\sqrt{a})(1-\sqrt{a})}=\frac{2a^2+4}{(1-a)(1+a)}-\frac{2}{1-a}\)
\(=\frac{2a^2+4}{(1-a)(1+a)}-\frac{2(1+a)}{(1-a)(1+a)}=\frac{2a^2-2a+2}{(1-a)(1+a)}=\frac{2(a^2-a+1)}{1-a^2}\)
\(\left(x^2-2y\right)^2+\left(x-\dfrac{1}{2}y\right)\left(x+\dfrac{1}{2}y\right)\)
\(=\left(x^2\right)^2-2.x^2.2y+\left(2y\right)^2+\left(x^2-\left(\dfrac{1}{2}y\right)^2\right)\)
\(=x^4-4x^2y+4y^2+x^2-\dfrac{y^2}{4}\)
\(=x^4-4x^2y+x^2+\dfrac{15y^2}{4}\)