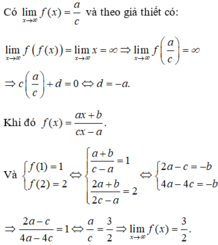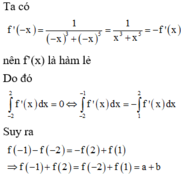f(x)=ax+b biết f1=-2: f2= -1. Tìm a,b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





a ) Ta có : f(2) = 5
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(2\right)\\\text{ax}-3=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\a.2-3=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\a=4\end{cases}}\)
Vậy a = 4
b ) Ta có : f(0) = 3
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(0\right)\\\text{ax}+b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\a.0+b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\b=3\end{cases}}\) ( 1 )
Ta có : f ( 1 ) = 4
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(1\right)\\\text{ax}+b=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\a.1+b=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\a+b=4\end{cases}}\) ( 2 )
Thay b = 3 ở ( 1 ) vào a+b=4 ở ( 2 ) ta được : a + 3 = 4
a = 1
Vậy a = 1 ; b = 3

Phương pháp:
- Lấy nguyên hàm hai vế từ đẳng thức đạo hàm và kết hợp điều kiện tìm f(x)
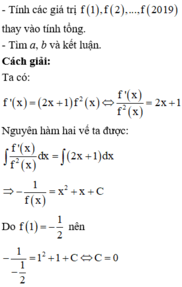


Chọn A.
Phương pháp: Sử dụng các công thức tính nguyên hàm đã biết.
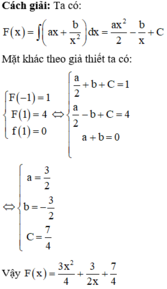

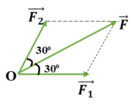
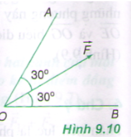
Áp dụng quy tắc hình bình hành: Từ điểm ngọn của vecto F lần lượt vẽ các đoạn song song với hai phương OA và OB ta được các vecto F1 trên OA và F2 trên OB sao cho
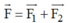
Hình bình hành có đường chéo cũng là đường phân giác của 1 góc nên nó là hình thoi.
Suy ra: F1 = F2
Mà
![]()
![]()