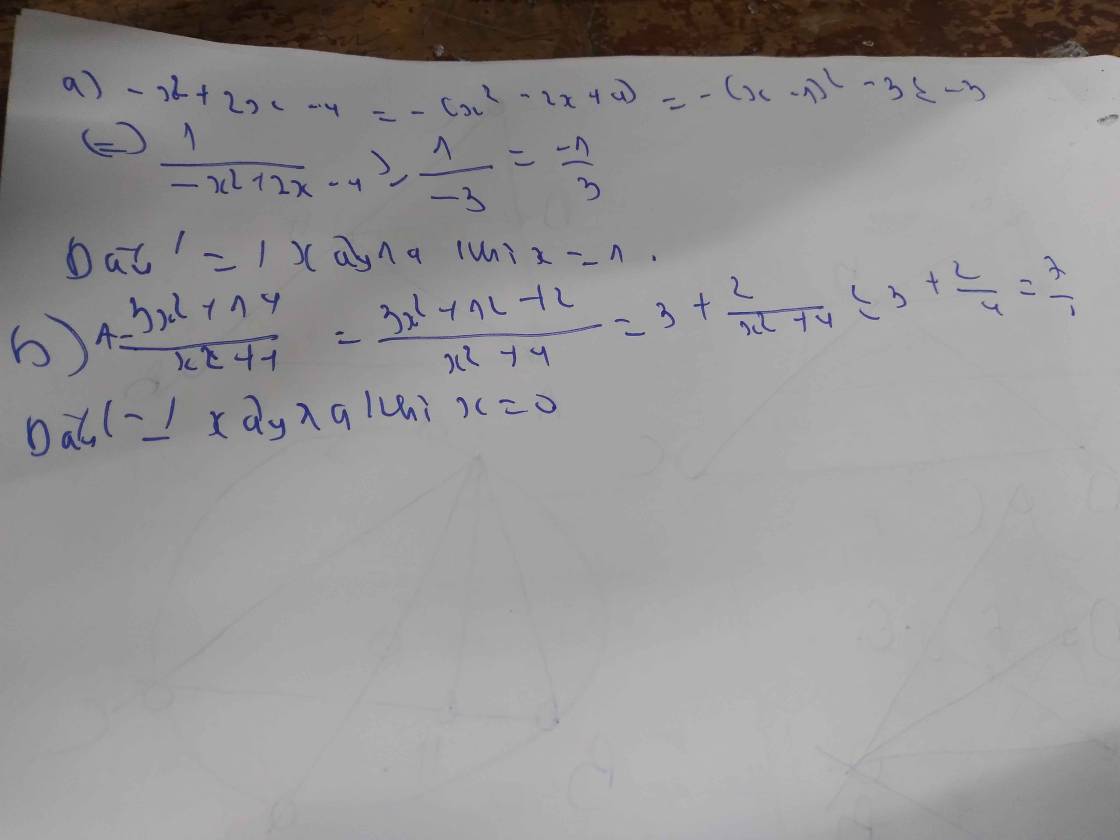Tìm GTNN A=(x-1)(2x-1)(2x^2-3x-1)+2017
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt : P = \(\left(x-1\right)\left(2x-1\right)\left(2x^2-3x-1\right)+2017\)
\(=\left(2x^2-3x+1\right)\left(2x^2-3x-1\right)+2017\)
\(=\left(2x^2-3x\right)^2+2016\ge2016\)
Dấu "=" xảy ra <=> \(2x^2-3x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{3}{2}\end{cases}}\)
Vậy GTNN của P là 2016 đạt tại x = 0 hoặc x = 3/2


a, A = (x^2-3x)^2 - 1 >=-1
Dấu "=" xảy ra <=> x^2-3x = 0 <=>x.(x-3) = 0 <=> x=3 hoặc x=0
Vậy Min A = -1 <=> xz=3 hoặc x=0
b, Đề thiếu kìa bạn ơi

1,2 kiểu gì ẹ
3,
\(\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1}\ge2\)
=> \(\frac{1}{x+1}\ge\frac{y}{y+1}+\frac{z}{z+1}\ge2\sqrt{\frac{yz}{\left(y+1\right)\left(z+1\right)}}\)
Làm tương tự rồi nhân lại ta được \(\frac{1}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\ge\frac{8xyz}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
=> \(xyz\le\frac{1}{8}\).Dấu bằng khi x=y=z=1/2
4.
Ta đi CM: \(\sqrt{\frac{a^3}{a^3+\left(b+c\right)^3}}\ge\frac{a^2}{a^2+b^2+c^2}\) <=> \(a^4+a\left(b+c\right)^3\le\left(a^2+b^2+c^2\right)^2\)
<=> \(a\left(b+c\right)^3\le2a^2\left(b^2+c^2\right)+\left(b^2+c^2\right)^2\)
Áp dụng BDT COSI thì
\(2a^2\left(b^2+c^2\right)+\left(b^2+c^2\right)^2\ge a^2\left(b+c\right)^2+\frac{\left(b+c\right)^2}{4}\ge a\left(b+c\right)^3\)
Do đó có dpcm
Làm tương tự rồi cộng lại ta đc bdt ban đầu
Dấu bằng xảy ra khi a=b=c