Tứ giác ABCD có: AB2 + CD2 = BC2 + AD2
Chứng minh: SABCD = 1/2*AC*BD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(AB^2+CD^2-\left(BC^2+DA^2\right)=\overrightarrow{AB}^2+\overrightarrow{CD}^2-\overrightarrow{BC}^2-\overrightarrow{AD}^2\)
\(=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{AB}-\overrightarrow{AD}\right)+\left(\overrightarrow{CD}-\overrightarrow{BC}\right)\left(\overrightarrow{CD}+\overrightarrow{BC}\right)\)
\(=\overrightarrow{DB}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)+\overrightarrow{DB}\left(\overrightarrow{BC}+\overrightarrow{DC}\right)\)
\(=\overrightarrow{DB}\left(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{BC}+\overrightarrow{DC}\right)\)
\(=2\overrightarrow{AC}.\overrightarrow{DB}\) (đpcm)

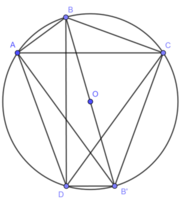
Kẻ đường kính BB’. Nối B’A, B’D, B’C.
Ta có: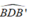 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ AC // B'D ( cùng vuông góc với BD)
Suy ra, tứ giác ADB’C là hình thang
Vì ADB’C nội tiếp đường tròn (O) nên ADB’C là hình thang cân
⇒ CD = AB'
⇒ A B 2 + C D 2 = A B 2 + A B ' 2
Mà tam giác BAB’ vuông tại A do 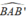 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ A B 2 + C D 2 = A B 2 + A B ' 2 = 2 R 2 = 4 R 2 (đpcm)

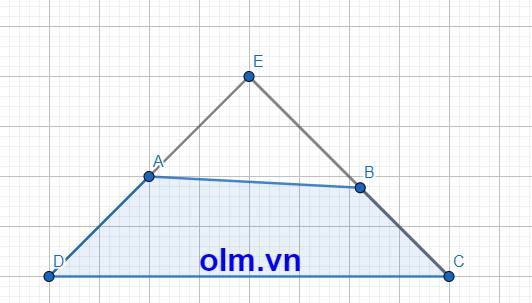
Kéo dài DA và CB lần lượt về phía A và B cắt nhau tại E
Xét tam giác DCE có \(\widehat{DEC}\) = 1800 - (\(\widehat{EDC}\) + \(\widehat{ECD}\)) = 1800- 900 = 900
⇒\(\Delta\)DEC vuông tại E
Xét \(\Delta\)AEB Theo pytago ta có: AE2 + BE2 = AB2
Tương tự ta có: DE2 + CE2 = DC2
Cộng vế với vế ta có: AE2 + BE2 + DE2 + CE2 = AB2+DC2
AE2 + CE2+BE2+DE2 = AB2+DC2 (1)
Xét \(\Delta\)AEC theo pytago ta có: AE2+ CE2 = AC2
Tương tự ta có: BE2 + DE2 = BD2
Cộng vế với vế ta có: AE2 + CE2 + BE2+ DE2 = AC2 + BD2 (2)
Từ (1) và (2) ta có: AC2 + BD2 = AB2 + DC2(đpcm)

cô làm rồi em ơi https://olm.vn/cau-hoi/bai-3-tu-giac-abcd-co-goc-c-goc-d-90-do-chung-minh-rang-ac2-bd-ab2cd2.8140260328277

Ta có: \(AC^2+BD^2=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)^2+\left(\overrightarrow{BC}+\overrightarrow{BA}\right)^2\)
\(=AB^2+AD^2+2\overrightarrow{AB}.\overrightarrow{AD}+BC^2+BA^2+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=AB^2+AD^2+BC^2+AD^2+2\overrightarrow{AB}\left(\overrightarrow{AD}-\overrightarrow{BC}\right)\)
\(=AB^2+AD^2+BC^2+AD^2\)

Câu 20: Tam giác ABC vuông tại B suy ra:
A. AC2 = AB2 + BC2 B. AC2 = AB2 - BC2
C. BC2 = AB2 + AC2 D. AB2 = BC2 + AC2
Câu 21: Tam giác ABC có BC = 5cm; AC = 12cm; AB = 13cm. Tam giác ABC vuông tại đâu?
A. Tại B B. Tại C
C. Tại A D. Không phải là tam giác vuông
Câu 22: Cho ABC có = 900 ; AB = 4,5 cm ; BC = 7,5 cm. Độ dài cạnh AC là:
A. 6,5 cm B. 5,5 cm C. 6 cm D. 6,2 cm
Câu 23: Tam giác nào là tam giác vuông trong các tam giác có độ dài các cạnh là:
A. 3cm, 4dm, 5cm. B. 5cm, 14cm, 12cm.
C. 5cm, 5cm, 8cm. D. 9cm, 15cm, 12cm.
Câu 24: Cho ABC có AB = AC và = 600, khi đó tam giác ABC là:
A. Tam giác vuông B. Tam giác cân
C. Tam giác đều D. Tam giác vuông cân
Câu 25: Nếu A là góc ở đáy của một tam giác cân thì:
A. ∠A ≤ 900 B. ∠A > 900 C. ∠A < 900 D. ∠A = 900