Cho hình chóp S.ABC. Trên các cạnh SA, SB, AC lần lượt lấy các điểm M, N, P không trùng với các đỉnh của hình chóp. Chứng minh rằng \(\dfrac{V_{S.MNP}}{V_{S.ABC}}=\dfrac{SM.SN.SP}{SA.SB.SC}\) (V là kí hiệu của thể tích)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


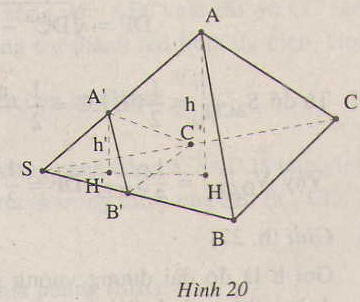
Gọi h và h’ lần lượt là chiều cao hạ từ A, A’ đến mặt phẳng (SBC).
Gọi S1 và S2 theo thứ tự là diện tích các tam giác SBC và SB’C’.
Khi đó ta có h′h=SA′SAh′h=SA′SA và 12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC
Suy ra VS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SCVS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SC
Đó là điều phải chứng minh.

Đáp án C
Ta có:
V S . M N P V S . A B C = S M S A . S N S B . S P S C = 1 12
⇒ V S . M N P = a 3 24

Thầy gợi ý cách xác định thiết diện thông qua hình vẽ sau:
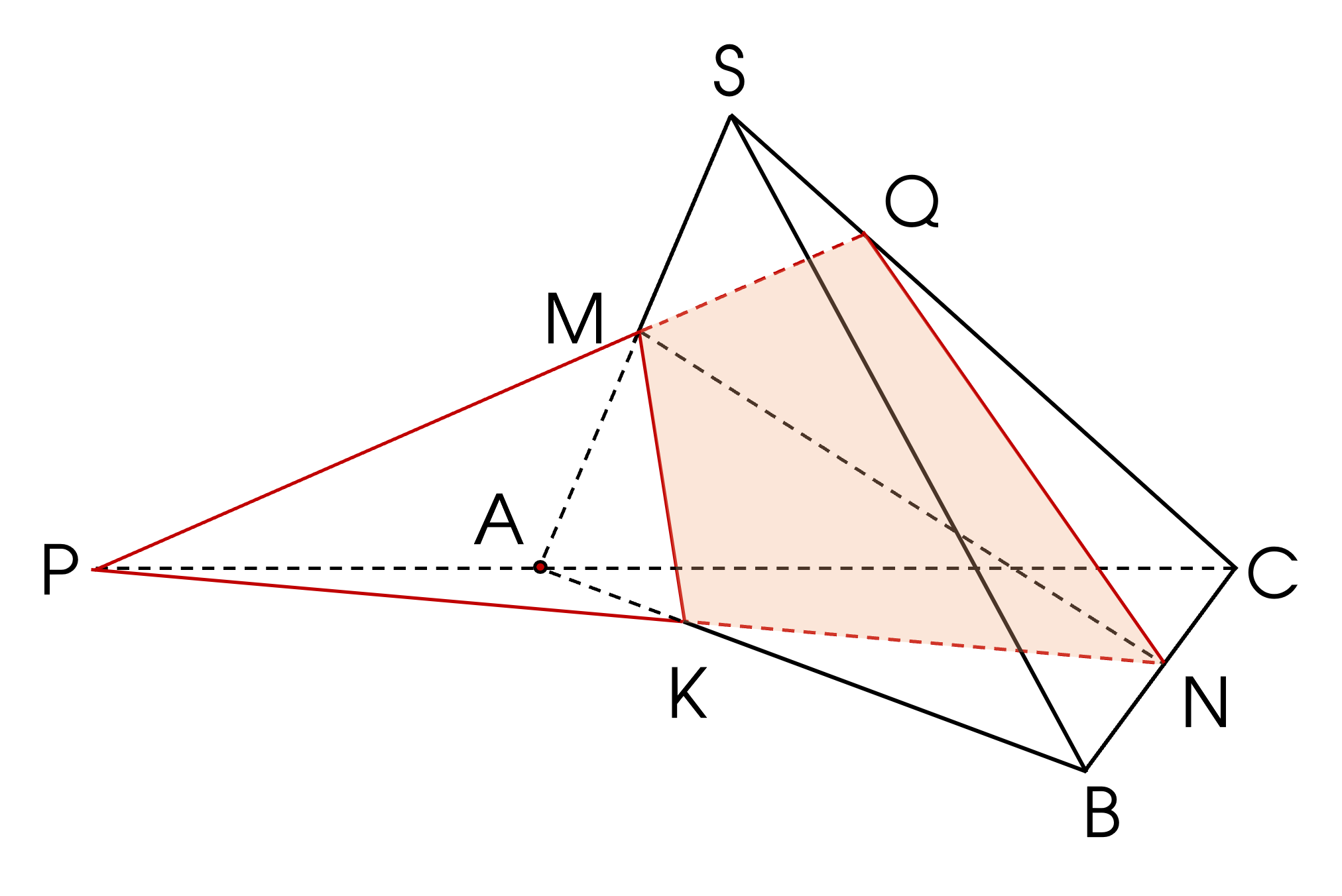
Em kéo dài KN cắt AC tại P (trong mp(ABC)), từ đó tiếp tục dựng hình để xác định giao tuyến với các mặt còn lại của hình chóp để có thiết diện là tứ giác KMQN nhé

Đáp án là B
Theo công thức tỉ số thể tích của hình chóp tam giác ta có
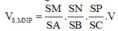
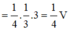

Đáp án A
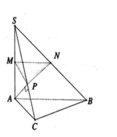
Xét tam giác SAC vuông tại A có AP là đường cao, ta có:
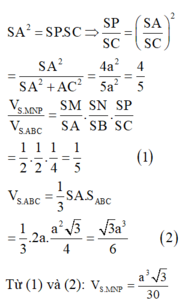
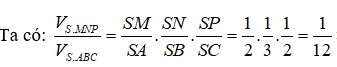
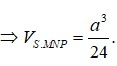

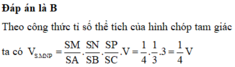
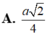
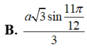


ms thi cấp 3 xong đúng ko?? có bài nào kt kì 1 thì cho mk nhé