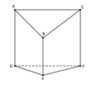
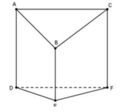
cho tam giác abc có các đường phân giác ad,be,cf tính số đo góc bac biết rằng tam giác def vuông tại d
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
1
13 tháng 4 2023
góc ABC+góc ACB=180-60=120 độ
=>góc IBC+góc ICB=60 độ
=>góc EIC=60 độ
CM
26 tháng 8 2017
Đáp án B
 |
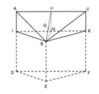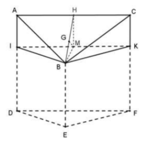
Góc giữa mặt phẳng (ABC) và (DEF) bằng với góc giữa 2 mặt phẳng (ABC) và (BIK) trong đó mặt phẳng (BIK) song song với (DEF)
Vẽ đường cao BH của tam giác đều ABC, suy ra H là trung điểm AC và BH = a 3 2
Gọi M là trung điểm IK. Khi đó HM là đường trung bình của hình chữ nhật AIKC
HM =AI = a 2 và HM song song với AI
Trong mặt phẳng (BHM) vẽ MG ⊥ BH tại G
Do MG ⊥ BH và AC ⊥ MG(AC ⊥ (BHM)) nên MG ⊥ (ABC) (2)
Từ (1) và (2) => góc giữa 2 mặt phẳng (ABC) và (BKI) bằng góc giữa MG với HM, tức góc HMG
Trong ∆ B H M vuông tại M, ta có:
CM
9 tháng 9 2019
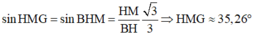
Vẽ đường cao BH của tam giác đều ABC, suy ra H là trung điểm AC và B H = 3 2 a
Gọi M là trung điểm IK. Khi đó HM là đường trung bình của hình chữ nhật AIKC
Chọn B
16 tháng 6 2018
a) Ta có AD là phân giác ^BAC, DE và DF lần lượt vuông góc AB;AC nên DE=DF
Xét \(\Delta\)AFD vuông tại F có ^DAF=1/2^BAC=600 => ^ADF=300
Tương tự tính được: ^ADE=300 = >^ADF+^ADE=^EDF=600
Xét \(\Delta\)DEF: ^EDF=600; DE=DF => \(\Delta\)DEF là tam giác đều.
b) Dễ thấy ^CAM=1800-^BAC=600.
CM // AD => ^ACM=^DAC=1/2^BAC=600
Từ đó suy ra \(\Delta\)ACM là tam giác đều.
c) Do \(\Delta\)ACM đều => CM=AC => CM-CF=CA-CF=AF
=> a - b = AF. Lại có: Tam giác AFD là tam giác nửa đều => AF=1/2AD
=> a - b = 1/2AD => AD= 2(a - b).
Vậy .........